Модель Харрода-Домара

В модели делаются следующие предпосылки:

1.Рассматривается закрытая экономика (NX= 0).

2.В экономике отсутствует государственный сектор (G = 0).

3.Инвестиции вводятся мгновенно, то есть отсутствует инвестиционный лаг (ΔK(t) = I(t)).

4.Отсутствует технический прогресс.

5. Прирост выпуска пропорционален приросту запаса капитала с коэффициентом пропорциональности 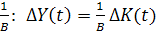, где В – коэффициент приростной капитаемкости (s w:val="28"/></w:rPr><m:t>)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 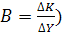, который показывает прирост запаса капитала, необходимый для приращения выпуска на единицу, является коэффициентом приростной капиталоотдачи: .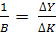

6.B и, соответственно, 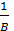не меняются во времени.

Обозначим норму накопления в момент t через α_t 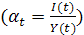, а норму потребления через .

Основное тождество национальных счетов в момент t имеет вид:

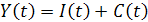
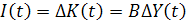
В непрерывном случае:

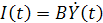
Отсюда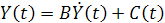

В модели Харрода-Домара рассматриваются три сценария экономического роста в зависимости от характера динамики потребления.

Случай 1. Потребление отсутствует, весь доход тратится на накопление

Эта гипотеза нереалистична, но позволяет дать оценку максимально возможного для данной экономики темпа роста доходов. При этом варианте

(5.1)

Решение (5.1) указывает на траекторию изменения доходов в этом случае:

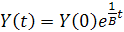
(5.2)

Из (5.2) вытекает, что 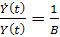, то есть максимально возможный темп прироста дохода в случае, когда весь доход тратится на накопление, равен приростной капиталоотдаче. Поэтому часто называют непрерывным «технологическим» темпом прироста дохода.

Случай 2. Уровень потребления не зависит от времени

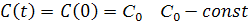
Тогда

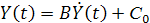
(5.3)

Из решения уравнения (5.3) следует, что:

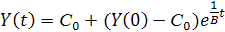
(5.4)

Условие (5.4) описывает траекторию роста дохода в случае, когда уровень потребления не изменяется во времени. Тогда норма накопления:

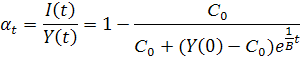
При .

Темп прироста национального дохода 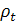, в этом случае равен:

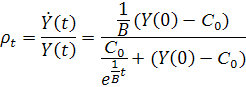
(5.5)

Из (5.5) следует, что при . Иначе говоря, в предельном случае доля потребления уменьшается до нуля и темп прироста совпадает с непрерывным «технологическим» темпом.

Случай 3. Потребление растет с настоянным темпом r

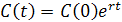
Тогда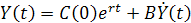

Этот сценарий обычно рассматривается в 3-х вариантах.

Случай 3.1. Потребление растет с темпом, равным технологическому темпу прироста дохода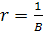

Тогда

В этом случае траектория роста дохода имеет вид:

(5.6)

Доход растет до тех пор, пока уровень накопления остается положительной величиной, так как если 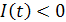, то и, следовательно .

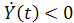Для того чтобы определить интервал времени, в течение которого доход растет, необходимо, следовательно, решить уравнение:

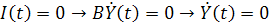
Из (5.6) вытекает, что

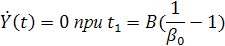
Где

Из (5.6) также можно получить, что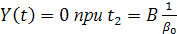

Таким образом, в случае, когда потребление растет с постоянным темпом, равным технологическому темпу прироста, доход растет в промежутке 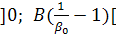, достигает своего максимального значения 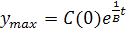в момент , а затем начинает падать и становится равным 0 в момент

Рис. 5.1 иллюстрирует траектории изменения дохода и накопления в случае 3.1.

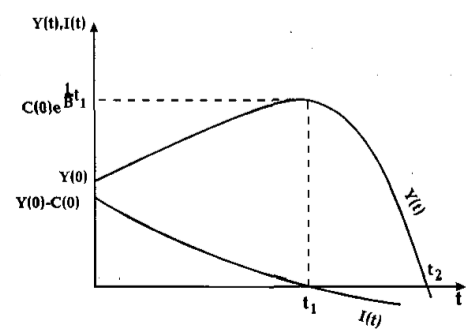
Рис.5.1

Случай 3.2. Потребление растет с постоянным темпом, превышающим технологический темп прироста

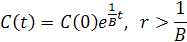
Тогда

(5.7)

Решение (5.7) показывает траекторию изменения дохода:

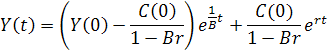
(5.8)

Из (5.8) вытекает, что темп прироста дохода в первоначальный момент времени равен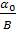

Таким образом, первоначальный темп прироста дохода положителен. Однако первое слагаемое в (5.8) положительно, а второе - отрицательно, поэтому этот случай аналогичен Случаю 3.1: сначала доход будет расти, а с некоторого момента начнет падать и в итоге упадет до 0.

Случай 3.3. Потребление растет с постоянным темпам, меньшим, чем технологический темп прироста

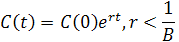
Это означает, что в (5.8) первое слагаемое может быть больше 0, меньше 0 или равно 0.

Случай 3.3.1. Темп прироста потребления меньше первоначального темпа прироста дохода

Пусть в (5.8)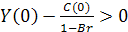

тогда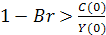

следовательно,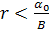

Таким образом, если темп роста потребления меньше темпа прироста дохода в первоначальный момент времени, 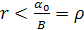, то в (5.8) оба слагаемых положительны и доход неограниченно растет во времени.

При 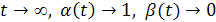, то есть в предельном случае норма накопления равна 1, а потребления - 0. Такой тип развития («накопление ради накопления») может быть целесообразным только на ограниченном отрезке времени.

Случай 3.3.2. Потребление растет с постоянным темпом, меньшим технологического темпа прироста и равным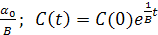

Тогда из (5.8)

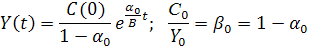
Следовательно,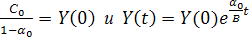

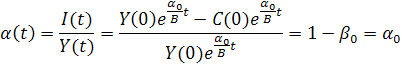
Другими словами, в этом случае норма накопления постоянна, а темп прироста национального дохода прямо пропорционален этой норме накопления и обратно пропорционален приростной капиталоемкости.

Случай 3.3.3. Темп прироста потребления больше первоначального темпа прироста

Из (5.8) вытекает, что в этом случае доход в некоторый момент перестанет расти и затем уменьшится до нуля.

Таким образом, модель Харрода-Домара указывает на случай 3.3.2. как на наиболее разумный вариант экономического развития. При этом варианте потребление и накопление растут с постоянным темпом, причем темп прироста национального дохода также постоянен и равен .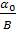

Из модели Харрода-Домара следует, что постоянного сбалансированного роста можно достичь двумя путями. Либо в начальный момент выбирается норма накопления , и тогда ищется оптимальный темп роста потребления r, который будет равен 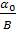. Либо выбирается желаемый темп роста потребления r, и тогда норма накопления, при которой можно достичь такого темпа, равняется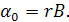

Интересно, что в этом случае потребление и доход в долгосрочном периоде растут с одинаковым темпом 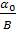, и потребление составляет постоянную часть от дохода, то есть функция потребления совпадает с функцией Кейнса в долгосрочном периоде, когда средняя склонность к потреблению не меняется.

С помощью модели Харрода-Домара среди возможных вариантов развития определяется наиболее предпочтительный, однако она не объясняет детерминант экономического роста. Эти детерминанты подробно анализируются в модели Солоу.

Date: 2015-10-19; view: 994; Нарушение авторских прав