Закон нормального распределения

Закон нормального распределения находит большое применение в различных отраслях техники. Этому закону подчиняются, многие непрерывные случайные величины, встречающиеся в технике, например ошибки измерения, высота микронеровностей на обработанной поверхности и многие другие. Широкое применение закона нормального распределения в технике находит свое теоретическое обоснование в теореме Ляпунова.

Опуская строгую математическую формулировку теоремы Ляпунова и ее доказательства ввиду их сложности, ограничимся лишь описанием следствия из этой теоремы, которое заключается в следующем.

Если случайная величина X представляет сумму очень большого числа взаимно независимых случайных величин х₁, х₂, …, х_n, влияние каждой из которых на всю сумму ничтожно мало, то независимо от того, каким законам распределения подчиняются слагаемые х₁, х₂, …, х_n, сама величина X будет иметь распределение вероятностей, близкое к нормальному, и тем точнее, чем больше число слагаемых.

Плотность вероятности или дифференциальная функция распределения случайной величины непрерывного типа, подчиняющейся закону нормального распределения, имеет следующее выражение:

Дифференциальная функция нормального распределения графически выражается в виде кривой холмообразного типа (рис. 11).

Из вида кривой нормального распределения следует, что она симметрична относительно ординаты точки х = , т. е. равновозможны одинаковые положительные и отрицательные отклонения от .

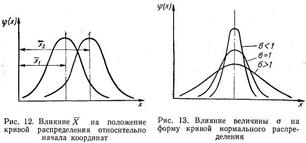Положение кривой относительно начала координат, и ее форма определяются двумя параметрами и s. С изменением форма кривой не изменяется, но изменяется ее положение относительно начала координат (рис. 12). С изменением s положение кривой не изменяется, но изменяется ее форма. С уменьшением s кривая становится более вытянутой, а ветви ее сближаются; с увеличением s, наоборот, кривая становится более приплюснутой, а ветви ее раздвигаются шире (рис. 13).

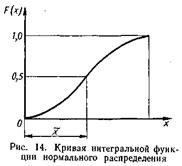
Интегральный закон нормального распределения выражается в общем виде так:

Интегральная кривая нормального распределения представлена на рис. 14.

Если случайная величина х следует нормальному закону, то достоверно, что она может принимать любые численные значения в пределах ±¥, поэтому

Вероятность 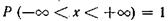представляет собой площадь под дифференциальной кривой нормального распределения. Очевидно, что вероятность значений х в любом другом интервале x₁ – х₂ (см. рис. 11) меньше единицы и будет равна

Произведем замену переменной х путем подстановки

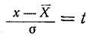
и, учитывая, что х = ts + ; dx = s dt, получим

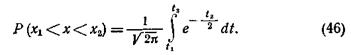
Новые пределы интегрирования и заменили пределы x₁ и х₂. Правую часть уравнения (46) можно представить в виде суммы двух интегралов:

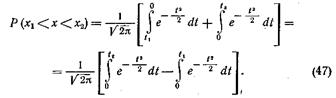
Знак плюс в уравнении (47) изменился на минус вследствие изменения пределов интегрирования с t₁ — 0 на 0 — t₁.

Интеграл носит название нормированной функции Лапласа и его значения для различных 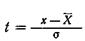приведены в таблицах.

Для практического использования закона нормального распределения необходимо зону рассеивания случайной величины х: ограничить конечными пределами. В технике и многих других прикладных науках считают, что практическая зона рассеивания случайной величины х, подчиняющейся закону нормального распределения, лежит в пределах ± 3s, т. е. в пределах 6s (см. рис. 11).

Date: 2015-10-19; view: 609; Нарушение авторских прав