Коэффициенты корреляции и детерминации

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии таким показателем является линейный коэффициент корреляции. Существует несколько видов формулы линейного коэффициента корреляции, основные из них представлены ниже:

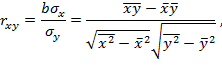
где 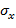и - среднее квадратическое отклонение x и y соответственно.

Линейный коэффициент корреляции, как известно, всегда находится в следующих пределах: -1≤ r_xy ≤1. Знак коэффициента регрессии определяет знак коэффициента корреляции. Если b < 0, тогда -1≤ r_xy ≤0, и наоборот, если b > 0, тогда 0≤ r_xy ≤1. Чем ближе значение коэффициента корреляции по модулю | r_xy | к единице, тем теснее связь между признаками в линейной форме. Однако, если абсолютная величина коэффициента корреляции близка к нулю, то это означает, что между рассматриваемыми признаками отсутствует линейная связь. При другом виде уравнения регрессии связь может оказаться достаточно тесной.

Для оценки качества подбора линейного уравнения регрессии находят также квадрат коэффициента корреляции, называемый коэффициентом детерминации R² = (r_xy)². Он отражает долю вариации результативного признака, объясненную с помощью уравнения регрессии, или, иными словами, долю дисперсии результата, объясненную регрессией, в общей дисперсии y:

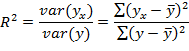
Следовательно, величина (1-R²) характеризует долю вариации, или долю дисперсии результата у, вызванную влиянием всех остальных, не учтенных в модели факторов. Значения коэффициента детерминации могут изменяться от нуля до единицы (0 ≤ R² ≤ 1). Например, R²=0,94 означает, что уравнением регрессии объясняется 94% дисперсии результативного признака, а прочими, не учтенными в модели факторами - 6%. Чем ближе коэффициент детерминации к единице, тем меньше роль других факторов и линейное уравнение регрессии описывает лучше исходные данные.

Date: 2015-10-19; view: 484; Нарушение авторских прав