К лабораторной работе № 3.21p

Дальневосточный федеральный университет

Школа естественных наук

ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКА В ВОЗДУХЕ

С ИСПОЛЬЗОВАНИЕМ БЛОКА COBRA 3

Учебно-методическое пособие

к лабораторной работе № 3.21p

по дисциплине «физический практикум»

11200.62 – «физика»

Составители

Полищук Виталий Ефремович

Полищук Раиса Федоровна

Владивосток

Издательский дом Дальневосточного федерального университета

Краткая теория работы. В физике приходится иметь дело с разными по своей природе волнами: механическими, тепловыми, электромагнитными и т.д. Несмотря на различную физическую природу этих волн, закономерности, которыми оп­ределяется их распространение, имеют между собой много общего и в основ­ном могут быть изучены на примере механических волн. В физике волной называют всякое изменяющееся со временем пространственное чередо­вание (колебание) максимумов и минимумов любой физической величины, на­пример плотности вещества, напряженности электрического поля, темпера­туры. Процесс распространения колебаний в пространстве называют вол­ной или волновым процессом. В случае механических волн распространение колебаний обусловлено взаимодействием между частицами твердой, жидкой или газообразной среды. Если взаимосвязь между частицами среды осуществ­ляется силами упругости, возникающими вследствие деформации среды при передаче колебаний от одних частиц к другим, то волны называются упругими. Наличие сплошной упругой среды является абсолютным требованием только для механических волн. К ним относятся звуковые, ультразвуковые, сейсмические и другие волны. Электромагнитные волны могут распространяться и в вакууме.

В зависимости от того, как колебания частиц среды ориенти­рованы относительно направления их распространения, механические волны подразделяются на поперечные и продольные. Являются ли волны, распространяющиеся в среде, продольными или поперечными – зависит от уп­ругих свойств среды. Если среда характеризуется упругими деформациями сдвига, то в такой среде будут распространяться поперечные волны, а если среда характеризуется упругими деформациями растяжения (сжатия), то в такой среде будут распространяться продольные волны. В жидкости и газе распространяются только продольные волны. В твердых телах продольные волны могут существовать наряду с поперечными. Скорость распространения продольных волн, определяется модулем Юнга E для данной среды и ее плотностью , а для поперечных волн – модулем сдвига G и плотностью среды : V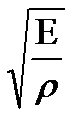_׀׀ = , V_┴ = .

Продольные и поперечные механические волны – частные случаи волнового процесса. Есть волны, в которых колебательное движение складывается из одновременных продольных и поперечных смещений (волны вздутия, поверхностные волны – волны на поверхности озер, морей и океанов).

Волны могут иметь различную форму. Одиночной волной, или импульсом волны, называется сравнительно короткое возмущение, не имеющее регу­лярного характера (рис.1,а). Ограниченный ряд повторяющихся возмущений называется цугом волны (рис.1,б). Особое значение в теории волн имеет представление о гармонических волнах, т.е. бесконечной сину­со­и­дальной (косинусоидальной) волне, в которой все изменения состояния среды, при распространении волны, происходят по закону синуса или косинуса (рис.1, в). Обычно понятие цуга относятся к отрезку синусоиды.

Область пространства, в котором при распространении волн частицы

-4-

среды совершают колебания, называют волновым полем. Геометричесое место точек, до которых к некоторому моменту времени дошло колебание, назы­вается фронтом волны, а ге­омет­ри­ческое место точек среды, ко­леблющихся в одинаковых фа­зах, называется волновой (или фазовой) поверх­но­стью. Фронт волны пред­ставляет собой поверхность, которая отделяет часть прост­ран­ства, уже вовлеченного в волновой процесс, от области, в которой колебания еще не возникли. Очевидно, что фронт волны является частным случаем волновой поверхности. В отличии от фронта волны, волновых поверхностей сущест­вует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Волновые поверхности остаются неподвижными (они проходят через положения равновесия частиц, колеблющихся в одинаковой фазе), а волновой фронт все время перемещается. Форма волновых поверхностей (фронта волны) определяет тип волн. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна называется плоской или сферической.

Уравнение волны. Уравнением волны называется выражение, связывающее смещение У колеблющейся частицы среды с ее координатами x, y, z и временем t:

У = У(x, y, z, t). (1)

Эта функция должна быть периодической как относительно времени t, так и от­носительно координат x,y,z. Периодичность по времени вытекает из того, что У описывает колебания частицы с координатами x, y, z. Периодичность по коор­динатам следует из того, что точки, отстоящие друг от друга на определенном расстоянии λ, называемом длиной волны, колеблются одинаковым образом.

Найдем эту зависимость для случая, когда в среде распространяется пло­ская синусоидальная волна в направлении оси х, т.е. найдем уравнение волно­вого луча. В этом случае, для продольных волн смещение колеблющихся точек среды Y(x,t) параллельно оси х, а для поперечных – перпендикулярно.

-5-

Пусть в начале координат (точка О, рис. 2) находится осциллятор (источник) гармонических колебаний. Колеба­ния такого источника имеют вид:

Y(0,t) = ASinwt, или Y(0,t) = ACoswt, где A-амплитуда гармонических колебаний (наибольшее от­кло­нение колеблющейся частицы от положения равновесия), w - циклическая частота колебаний, t – время, при котором наблюдается данное смещение Y(0,t) колеблющейся точки от положения равновесия. Если точка О совершает колебательное движение в упругой среде, то в среде будут распространяться эти колебания и через время t они достигнут точки М, удаленной от источника колебаний на расстояние х (рис. 2). При этом, колебания частиц среды имеют ту же частоту w, что и колебания источника волн. В точке М смещение Y(x, t) колеблющейся точки в любой момент времени t будет точно таким, каким оно было в точке О в момент времени (t-t), т.е.

Y(x, t) = Y(О,(t-t)) = ASinw(t-t). (2)

Если волна распространяется в среде со скоростью V, то время t = и тогда уравнение бегущей плоской волны в окончательном виде примет вид:

Y(x, t) = ASinw(t - ), (3)

где Y(x, t) – смещение колеблющейся точки волнового поля, удаленной от источника волны на расстояние x, в момент времени t; A – амплитуда волны; w - циклическая частота волны, которая связана с периодом волныT и частотой n - соотношениями: w = = n; выражение w(t - ) – называется фазой волны, Sin которой показывает, какую долю от амплитуды имеет смещение волны в точке x в момент времени t.

Если бы в точке О колебания совершались по закону Y(0,t) = ACoswt, то уравнение бегущей плоской волны имело бы вид

Y(x, t) = ACosw(t - ). (4)

Расстояние, на которое определенная фаза колебаний распространяется за время, равное одному периоду колебаний, называется длиной волны λ, при этом λ = VT. Так как период связан с частотой колебаний n соотношением , то скорость волны связана с длиной волны и частотой: V = λn.

Под скоростью распространения волны V подразумевается ее фазовая скорость, т.е. скорость распространения данной фазы монохроматической волны (волны, имеющей одну частоту). Наряду с фазовой скоростью волн существует так называемая групповая скорость. Групповая скорость относится к случаю распространения волн сложного (не синусоидального) характера в среде, где фазовая скорость распространения синусоидаль­ных волн зависит от их час­тоты. Зависимость фазовой скорости волн от их частоты называется дисперсией волн. Всякая реальная волна представляет собою наложение (группу) бесконечных синусоид (косинусоид), и скорость ее распространения в диспергирующей среде отличается от фазовой скорости слагаемых волн.

-6-

Эта скорость распространения реальных волн в диспергирую­щей среде и называется группо­вой скоростью.

Волновое уравнение. Уравнение любой волны представляет собой решение некоторого дифференциального уравнения движения, называемого волновым уравнением. Используя уравнение (3), можно вывести дифференциальное уравнение, описывающее распространение в среде волнового процесса. Для этого продифференцируем уравнение (3) дважды по каждой из переменных, т.е. по координате x и времени t.

= Aw×(- ) Cosw(t - ), (6) = -A w²×(- )² Sinw(t - ), (7)

= AwCosw(t - ), (8) 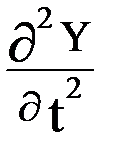= -A w²Sinw(t - ). (9)

При сравнении уравнений (7) и (9) видно, что их правые части отличаются множителем (- )². Откуда следует уравнение:

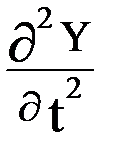= ()² (10)

Это дифференциальное уравнение (10) называется волновым уравнением. Оно описывает распространение незатухающего волнового процесса в среде (в данном случае при условии, что Y не зависит от y и z). В случае, когда Y=Y(x, y, z, t), это уравнение примет вид

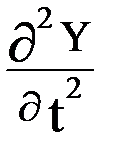()² = { + + }. (11)

Всякий раз, когда та или иная физическая величина оказывается зависящей от времени и координат и при этом ее частные производные связаны между собой волновым уравнением, можно утверждать, что процесс изменения этой величины представляет волну, распространяющуюся со скоростью V.

Волны, частоты колебаний частиц в которых лежат в пределах от 16 до 20000 Гц называются звуковыми или акустическими. Механические колебания с частотой выше 20 кГц называются ультразвуковыми. В отличие отзвуковых колебаний, они не воспринимаются человеческим ухом (как и колебания с частотами ниже 16 Гц – инфразвуковые). Ультразвуковые колебания, как и звуковые, могут распространяться в твердых, жидких и газообразных веществах.

В воздухе, как и во всяком другом газе, колебания распространяются в виде продольных волн. Достигнув нашего органа слуха – уха, колебания частоты от 20 до 20000 Гц воспринимаются им и только по этому свойству они выделены в особую группу звуковых или акустических колебаний (волн). Колебания 20 – 20000 Гц связаны только с физиологическими особенностями человеческого органа слуха. С физической же точки зрения эти колебания ничем специфическим не отличаются от колебаний до 20 Гц и более 20000 Г ц. Явления

-7-

связанные с возникновением и распространением звуковых волн называются акустическими явлениями.

Целью данной лабораторной работы является экспериментальное определение скорости звука в воздухе при комнатной температуре.

В рассматриваемой лабораторной работе скорость звука в воздухе определяется методом непосредственного измерения времени t распространения звуковой волны от источника колебаний до приемника и расстоянию между ними. Время распространения звука от источника до приемника определяется с помощью блока COBRA 3. Скорость звука определяется по формуле 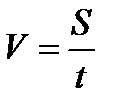(12), где S- расстояние между источником и приемником колебаний, t – время прохождения звуком расстояния S. Расстояние S определяется с помощью рулетки. На рисунке 3 показан внешний вид экспериментальной установки.

Рис.3.

Date: 2015-10-18; view: 719; Нарушение авторских прав