Графический метод (метод кинематических диаграмм)

Кинематические диаграммы - это графики функций перемещений, скоростей и ускорений характерных точек звеньев в зависимости от времени, т. e. S=S(t), V=V(t), a=a(t),

или j=j(t), w=w(t), e=e(t).

Цель исследования - построить эти графики. Достоинства:

а) наглядное представление изменения кинематических характеристик
за один цикл;

б) малая трудоемкость при исследовании простых механизмов.
Недостатки:

а) точность исследования зависит от масштаба построения и от квалификации исследователя;

б) большая трудоемкость при исследовании сложных механизмов.

Исследование начинается с построения плана положений механизма и траекторий движения центров тяжести звеньев.

Планом положений механизма называется графическое представление относительных положений его звеньев, построенное в определенном масштабе.

Масштабом физической величины называют длину отрезка в мм изображающую единицу измерения этой величины.

Например (рисунок 2.6). Длина звена l₁ = 0,1 м = 100 мм на чертеже изображается отрезком ₁ - 20 мм (в 5 раз меньше). М 1:5. Если длина звена

2 — 1₂ = 1000мм, тов масштабе построения 1₂ = 200мм.

В ТММ вместо понятия масштаб построения пользуются понятием масштабный коэффициент.

Масштабным коэффициентом называется отношение изображаемой единицы физической величины в свойственных ей единицах измерения к длине отрезка на чертеже в мм изображающего эту величину.

Чертежная длина звена 2 (рисунок 2.13)

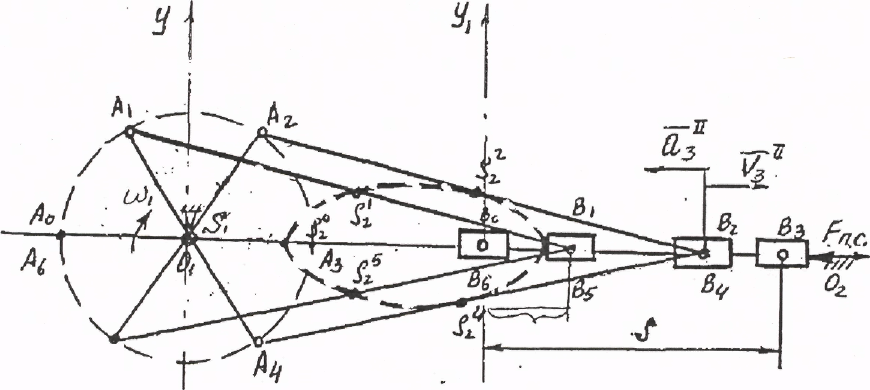
План положений начинают строить с исходного (нулевого) положения механизма. За нулевое положение принимается начало рабочего хода выходного звена - ползуна 3 (рисунок 2.7), начало преодоления силы полезного сопротивления - F_п._с.

Определяют нулевое положение построением нескольких пробных положений, методом засечек, пока ползун не окажется в крайнем (левом) положении, противоположном направлению силы полезного сопротивления.

Последовательность построения.

Разбиваем траекторию кривошипа на несколько частей, соответствующих равным интервалам времени (6, 12 или 24). При равно- мерном вращении кривошипа окружность будет разбита на равные части. Соединяем точку О₁ с размеченными положениями. Получаем соответствующие положения кривошипа A₀, A₁… A₆.

Методом засечек осуществляем разметку положений следующих звеньев 2 и 3. Точки В₀, В₃ - точки возврата ползуна (предельные положения).

Определяем траекторию движения центров тяжести звеньев механизма S₂ и S₃ относительно системы координат X и У.

Определим перемещение траектории центра тяжести ползуна - вдоль оси X в функции от времени

S₃= S₃(t).

Проводим две оси координат (рисунок 2.8а). На оси абсцисс откладывает отрезок произвольной длины - мм, представляющий собой в масштабе m_t время

Т (с) одного полного оборота первого звена (время цикла)

Рисунок 2.7

T=60/n₁=2p/w₁,

где n₁ - частота вращения первого звена в об/мин;

w₁ - угловая скорость первого звена в 1/с.

Масштабный коэффициент времени, с/мм

m_t =T/ =60/(n₁ ).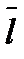

Отрезок 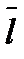разбиваем на 6 равных частей соответствующих шести положениям механизма.

По оси ординат из точек 0, 1, 2, 3, 4, 5, 6 откладываем величину перемещения центра тяжести S₃ вдоль оси X (рисунок 2.7).

Если эти отрезки откладывать прямо с плана положений механизма, то

масштабный коэффициент диаграммы перемещения центра тяжести

вдоль оси X будет равен масштабному коэффициенту построения плана

положений

Построение диаграммы скорости перемещения центра тяжести вдоль оси X, осуществляется методом графического дифференцирования по параметру времени.

Метод хорд. Соединяем точку О с точкой 1 хордой (рисунок 2.10а). Проводим новую систему координат для диаграмм скорости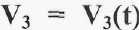

(рисунок 2.106). Продолжим ось абсцисс влево относительно начала координат и отложим на ней отрезок произвольной длины H1 (мм). Точка Р₁ называется полюсом графического дифференцирования.

Из полюса P1 проводим линию 01¹ параллельно хорде 01. Из подобия прямоугольных треугольников ОI1 и Р1 01¹ (рисунок 2.10а,б) следует

где 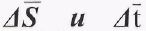- приращение функции и аргумента построенные в опреде­ленных масштабах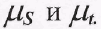

Рисунок 2.8

Истинное приращение функции и аргумента

и

откуда скорость на 1 участке

Подставим эти значения в равенство (2.1). Тогда

Поскольку величина 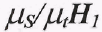представляет собой только масштабы построения, то отрезок с точностью до постоянного множителя изображает на диаграмме 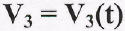среднюю скорость движения вдоль оси X на первом участке, построенную в определенном масштабе. Переносим ее в середину 1 участка.

Масштабный коэффициент графика скорости 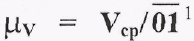или сравнивая с (2.2)

Соединяем точки 1 и 2 хордой (рисунок 2.10а). Из полюса Р проводим Р2¹, параллельно хорде 12. Отрезок 02¹ представляет собой среднюю скорость движения на участке 1-2. Переносим ее в середину 2 участке и т.д. Полученные точки соединяем плавной кривой -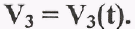

Дифференцируя график скорости 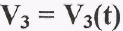получим график ускорения

центра тяжести 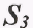вдоль оси X (рисунок2.10в)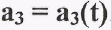

На первом участке графика скорости O-I находим точки пересечения графика с отметками времени и соединяем их хордой. Ось абсцисс графика ускорения продолжаем влево на произвольное расстояние Н₂ до точки Р₂. Точка Р₂ - полюс графического дифференцирования. Из точки Р₂ проводим линию параллельно хорде на первом участке графика скорости до пересечения с осью ординат. 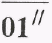Получаем точку По аналогии отрезок представляет собой в масштабе построения среднее ускорение на первом участке. Переносим ее в середину первого участка и т.д.

Полученные точки 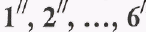соединим плавной кривой -т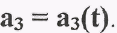

Масштабный коэффициент графика ускорения, (м/с)/мм

Проверка правильности построения диаграмм:

- там, где функция имеет экстремумы, производная равна 0;

- там, где функция меняет знак - производная имеет экстремумы.

Истинные значения скорости и ускорения для всех 12 положений

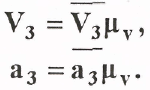
* Ассур Леонид Владимирович (1878-1920) опубликовал в 1914-1918 гг. «Исследование плоских стержневых механизмов с точки зрения их структуры и классификации»

Date: 2015-10-18; view: 563; Нарушение авторских прав