
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Показатели вариации
|
|
Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.
Исследование вариации в статистике имеет большое значение, помогает познать сущность изучаемого явления. Особенно актуально оно в период формирования многоукладной экономики. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию для принятия научно обоснованных управленческих решений.
Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом — эти отличия велики, т.е. в одном случае вариация признака мала, а в другом — велика, это имеет весьма важное значение для характеристики надежности средней величины.
Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот, — чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другие показатели, характеризующие отклонения отдельных значений от общей средней.
Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.
X К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.
X Самым элементарным показателем вариации признака является размах вариации R, представляющий собой разность между максимальным и минимальным значениями признака:
R= хmax - хmin
Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением ее размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и даёт обобщённую характеристику. Простейший показатель такого типа — среднее линейное отклонение.
X Среднее линейное отклонение  представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта:
представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта:  .
.
Среднее линейное отклонение:
• для несгруппированных данных  ,
,
где п - число членов ряда;
• для сгруппированных данных  ,
,
где åf — сумма частот вариационного ряда.
X Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
• простая дисперсия для несгруппированных данных
 ;
;
• взвешенная дисперсия для вариационного ряда
 ,
,
Формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).
Формулу для расчета дисперсии можно преобразовать,
учитывая, что  :
:
 ,
,
т.е. дисперсия равна разности средней из квадратов вариантов и квадрата их средней.
Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
 ,
,
где s - дисперсия, исчисленная по способу моментов;
i - величина интервала;
 - новые (преобразованные) значения вариантов
- новые (преобразованные) значения вариантов
(А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);
 - момент второго порядка;
- момент второго порядка;
 - квадрат момента первого порядка.
- квадрат момента первого порядка.
Дисперсия имеет большое значение в экономическом анализе. В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия. Ниже, в частности, будет показано разложение дисперсии на соответствующие элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений.
X Среднее квадратическое отклонение s равно корню квадратному из дисперсии:
· для несгруппированных данных  ,
,
• для вариационного ряда  ,
,
Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
 ,
,
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.
Пример. Рассмотрим расчет различными способами показателей вариации на примере данных таблицы:
| Группы п/тий по объему т/о, млн. руб | Число предприятий |
| f | |
| 170-190 | |
| 190-210 | |
| 210-230 | |
| 230-250 | |
| Итого |
Рассчитаем дисперсию по трем, приведенным выше формулам.
1. 
2. 
3. 
Исчислим средний объем товарооборота, млн. руб.:

ХАР = 21 600 / 100 = 216
Далее строим вспомогательную таблицу и делаем расчеты
| Группы п/тий по объему т/о, млн. руб | Число предпри- ятий | Середи-ны интерва-лов | Расчетные значения | |||||||
| f | x | f x | (x-x) | (x-x)2 | (x-x)2f | x2 f | x1 | x1 f | x12f | |
| 170-190 | 1 800 | - 36 | 1 296 | 12 960 | 324 000 | - 2 | - 20 | |||
| 190-210 | 4 000 | - 16 | 5 120 | 800 000 | - 2 | - 20 | ||||
| 210-230 | 11 000 | 2 420 000 | ||||||||
| 230-250 | 4 800 | 11 520 | 1 152 000 | |||||||
| Итого | - | 21 600 | - | - | 30 400 | 4 696 000 | - | - 20 |
Взяв расчетные данные из таблицы, подставляем их в наши формулы (1,2,3)
1.  = 30 400 / 100 = 304
= 30 400 / 100 = 304
2.  = 4 696 000/100 – (216)2 = 304
= 4 696 000/100 – (216)2 = 304
3. 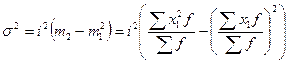 = 202 х (80/100 – (-20/100)2) = 304
= 202 х (80/100 – (-20/100)2) = 304
где А = 50 центральный вариант с наибольшей частотой
i = 20 - величина интервала данного ряда
Определим коэффициент вариации, %
 = 17,44 / 216 х 100 = 8
= 17,44 / 216 х 100 = 8
Таким образом предприятия достаточно однородны по товарообороту, поскольку вариация признака составляет лишь 8%.
Теперь выполним расчет дисперсии по разным формулам:
Date: 2015-10-18; view: 486; Нарушение авторских прав