
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Виды средних и способы их вычисления
|
|
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.
Средняя арифметическая
Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя. Так, например, общий фонд заработной платы — это сумма заработных плат всех работников, валовой сбор урожая — сумма произведенной продукции со всей посевной площади.
Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.
Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой, служит простая средняя.
X Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):
 ,
,
где х1, x2,..., хn - индивидуальные значения варьирующего признака (варианты);
п - число единиц совокупности.
Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).
Х Средняя арифметическая взвешенная — средняя сгруппированных величин х1, x2,..., хn — вычисляется по формуле:
 ,
,
где  - веса (частоты повторения одинаковых признаков);
- веса (частоты повторения одинаковых признаков);
 - сумма произведений величины признаков на их частоты;
- сумма произведений величины признаков на их частоты;
 - общая численность единиц совокупности.
- общая численность единиц совокупности.
Например, имеются данные о размере взносов учредителей
| Размер взноса каждого учредителя, тыс. руб. х | Число учредителей, чел. f | хf |
| Итого: |
По формуле вычислим среднюю арифметическую взвешенную:

ХАР = (180 + 320 + 270 + 500) / 15 = 1270 / 15 = 84,7 тыс. руб.
Если значения признака заданы в виде интервальных рядов (“от - до”), то при расчете средней арифметической величины в качестве значений признаков принимают середины этих интервалов, в результате чего получается дискретный ряд.
Например, рассмотрим следующий пример:
| Исходные данные | Расчетные значения | ||
| Группы работников по оплате труда, руб. | Число работников, чел. f | Середина интервала, руб. х | хf |
| До 1000 1000 - 1200 1200 - 1400 1400 - 1600 1600 - 1800 1800 и более | 4 500 | ||
| Итого | 145 800 |
Первый столбец является интервальным рядом, от него перейдем к дискретному путем замены интервальных значений их средними значениями (простая средняя между верхней и нижней границами каждого интервала). При этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним.
После того как найдены середины интервалов, вычисления делают так же - варианты умножают на частоты (веса) и сумму произведений делят на сумму частот (весов), руб.:

ХАР = 145 800 / 100 = 1458.
Итак средний уровень оплаты труда работников составляет 1458 руб. в месяц.
Средняя гармоническая
При расчете средних показателей помимо средней арифметической могут использоваться и другие виды средних. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем (например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и то же время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления.
Вид средней определяется характером взаимосвязи определяющего показателя с осредняемым.
Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака х и их частоты f.
Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение хf, применяется формула средней гармонической взвешенной. Чтобы исчислить среднюю, обозначим xf = w, откуда f = w/x. Теперь преобразуем формулу средней арифметической таким образом, чтобы по имеющимся данным х и w можно было исчислить среднюю. В формулу средней арифметической взвешенной (5.4) вместо xf подставим w, вместо f - отношение w/x и получим формулу средней гармонической взвешенной:
 ,
,
Из формулы видно, что средняя гармоническая - средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.
Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = хf, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.
Исчисление средней гармонической взвешенной по формуле освобождает от необходимости предварительного расчета весов, поскольку эта операция заложена в саму формулу.
Например, по данным таблицы определим среднюю цену 1 кг яблок:
| Номер магазина | Исходные данные | |
| Цена яблок, руб./кг, | Выручка от реализ, руб., | |
Среднюю цену 1 кг яблок по трем магазинам исчислим по формуле средней гармонической взвешенной:

ХГАР = (3060+2800+1920) / (3060/17+2800/20+1920/24) = 7780 / 400 = 19,45
Средняя геометрическая
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню
каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическая исчисляется извлечением корня степени и из произведений отдельных значений — вариантов признака х:
 ,
,
где n — число вариантов; П — знак произведения.
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.
Использование средней геометрической показано в гл. 7.
Средняя квадратическая и средняя кубическая
В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая и средняя кубическая. Формулы для расчета средней квадратической:
X средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
 ,
,
X средняя квадратическая взвешенная
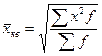 ,
,
где f — веса.
Формулы для расчета средней кубической аналогичны:
X средняя кубическая простая
 ,
,
X средняя кубическая взвешенная
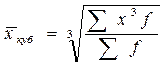 ,
,
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов х, и из их отклонений от средней  при расчете показателей вариации).
при расчете показателей вариации).
Структурные средние
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Х Мода m0 — значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду — вариант, имеющий наибольшую частоту.
Например, в таблице
| Размер взноса каждого учредителя, тыс. руб. | Число учредителей, чел. |
| Итого: |
наибольшей частотой является число 5, этой частоте соответствует модальное значение признака, т.е. размер взноса учредителей. Мода свидетельствует, что в данном примере больше всего учредителей которые внесли по 100 тыс. руб.
В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
 ,
,
где xm0 — нижняя граница модального интервала; iM0 — модальный интервал; fM0, fM0-1, fM0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно).
Пример. Модальный интервал определяется по наибольшей частоте.
| Группы предприятий по стоимости ОПФ, млн. руб. | Число предприятий |
| 14 -16 16 -18 18 -20 20 -22 22 - 24 | |
| Итого: |
По данным таблицы рассчитаем моду, млн. руб.:
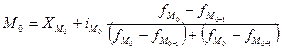
Мо= 18 + 2 х [ (10-6) / (10-6+10-4)] = 18,8
Итак модальным значением стоимости ОПФ предприятий региона является стоимость, равная 18,8 млн. руб.
X Медиана Мe - это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.
В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.
В интервальных рядах распределения медианное значение (поскольку оно делит всю совокупность на две равные по численности части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная частота (накопленная сумма частот) равна или превышает полусумму всех частот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:
 ,
,
где XMe — нижняя граница медианного интервала; iMe — медианный интервал; åf/2 - половина от общего числа наблюдений; SМe - сумма наблюдений, накопленная до начала медианного интервала; fMe - число наблюдений в медианном интервале.
Пример. Рассчитаем медиану по данным таблицы.
| Группы предприятий по стоимости ОПФ, млн. руб. | Число предприятий |
| 14 -16 16 -18 18 -20 20 -22 22 - 24 | |
| Итого: |
Прежде всего найдем медианный интервал, он должен превышать половину суммы всех частот (25:2=12,5), возьмем первый интервал 14-16, его частота равна 2, 2 меньше 12,5 (неподходит); возьмем второй интервал 16-18, его накопленная частота равна 2+6=8, 8 меньше 12,5, третий интервал 18-20, его накопленная частота 2+6+10 = 18, 18 превышает 12,5. Нижняя граница интервала 18 млн. руб., его частота 10, частота накопленная до него, равна 8.
Подставив данные в формулу, найдем значение медиан, млн. руб.

Ме = 18 + 2 х [(25/2 - 8) / 10] = 18,9
Полученный результат говорит о том, что из 25 предприятий региона 12 предприятий имеют стоимость ОПФ менее 18 млн. руб., а 12 предприятий - более.
Date: 2015-10-18; view: 540; Нарушение авторских прав