
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числа 3, 4, 5 в Кеплеровом учении о мировой гармонии. Как мы уже убедились, из первых 10 чисел числа 3, 4 и 5 имеют для нас особую важность
|
|
Как мы уже убедились, из первых 10 чисел числа 3, 4 и 5 имеют для нас особую важность.
3 – это число первичной божественной вибрации, вечного ритма развития.
4 – число земной реальности и основа нашей ориентации (стороны света).
5 – квинтэссенция и число человека.
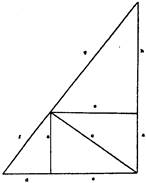 |
Кеплер в своем учении о мировой гармонии выводит из этих трех чисел несколько важных взаимосвязей. Изображенный внизу большой треугольник и все входящие в него маленькие имеют соотношение сторон 3:4:5. Если принять длину отрезков сторон за основание частоты звуковых колебаний, то мы получим семь тонов мажорной гаммы плюс соответствующие мажорные же трезвучия. Приняв длину отрезков за масштабное изображение длины струн музыкального инструмента, мы получим минорные трезвучия.
На этих числах – 3, 4 и 5 – строятся и единственные пять совершенных тел, известных геометрии (плато- новы тела). Это - тела, у всех поверхностей которых
есть общая средняя точка, сами же поверхности состоят из одинаковых граней (треугольников, четырехугольников и т.д.). Вот эти тела:
| тетраэдр | - четырехгранник (треугольная пирамида) |
| октаэдр | - восьмигранник |
| икосаэдр | - двадцатигранник, состоящий из треугольников |
| гексаэдр | - шестигранник (куб) из квадратов |
| додекаэдр | - двенадцатигранник (бриллиант) из пятиугольников |
Кеплер поместил эти тела одно в другое таким образом, что куб оказался вписан в наименьший из возможных шаров, а в куб тоже вписан шар соответствующего размера. В этот шар вписана треугольная пирамида, и у нее внутри тоже находится шар, в котором помещается двенадцатигранник, а в нем - опять шар, затем двадцатигранник, снова шар, восьмигранник - и последний, самый маленький шар. Так вокруг пяти тел образуются шесть шаров с единым центром. Если сравнить расстояния, отделяющие поверхность каждого шара от поверхности следующего, то они окажутся пропорциональны расстояниям между орбитами планет Солнечной системы от Меркурия до Сатурна:
| 1-й шар = Сатурн | в нем куб |
| 2-й шар = Юпитер | в нем четырехгранная пирамида |
| 3-й шар - Марс | в нем додекаэдр |
| 4-й шар = Земля | в нем икосаэдр |
| 5-й шар = Венера | в нем октаэдр |
| 6-й шар = Меркурий |

КЕПЛЕРОВА МОДЕЛЬ МИРОЗДАНИЯ
СО ВПИСАННЫМИ ДРУГ В ДРУГА
ПЛАТОНОВЫМИ ТЕЛАМИ.
Date: 2015-10-18; view: 487; Нарушение авторских прав