Статистический метод

Статистический метод описания в известной степени является обобщением двух предыдущих: динамического и термодинамического. В его основе лежат следующие представления:

- свойства системы в целом определяются свойствами и характером движения частиц, ее составляющих;

- в силу многочисленности частиц и большого числа столкновений их поведение носит случайный характер;

- поведение системы в целом необходимо описывать не совокупностью координат и скоростей частиц, а усредненными характеристиками (средняя энергия, средняя плотность и т.д.). При сопоставлении этих усредненных характеристик с термодинамическими соотношениями выясняется смысл микроскопических параметров системы. Так, например, оказалось, что абсолютная температура пропорциональна средней кинетической энергии поступательного движения молекул.

Закономерности, получаемые статистическим методом, называются вероятностными, или статистическими. Для их получения строится модель изучаемой системы.

Статистический метод в физике имеет широкое применение по двум причинам:

- большинство физических систем имеют огромное число частиц;

- поведение микрочастиц описывается статистическими закономерностями.

В данной работе рассматривается применение статистического метода описания к вопросу о распределении молекул газа по скоростям в состоянии равновесия, в отсутствие внешних силовых полей. Опыт показывает, что любая изолированная система приходит в состояние теплового (термодинамического) равновесия, в котором ее макроскопические параметры (давление, температура) не изменяются со временем и постоянны в объеме. Но согласно основным представлениям молекулярно-кинетической теории молекулы системы находятся в беспорядочном хаотическом движении. В идеальном газе молекулы движутся между столкновениями поступательно с разными скоростями, изменяя скорость при столкновении. В этом случае случайной величиной (разной у молекул) является скорость и стоит задача о нахождении распределения молекул газа по скоростям. Для этого необходимо принять модель системы и качественно рассмотреть свойства этой системы в состоянии теплового равновесия.

Так как в состоянии равновесия давление во всех частях системы одинаково, то естественно допустить, что в газе отсутствуют какие-либо направленные движения молекул, то есть движения молекул предельно неупорядочены. В отношении скоростей молекулы это означает:

- скорость молекул и ее проекции являются непрерывными величинами, так как ни одно значение скорости не имеет преимущества перед другими значениями;

- при тепловом равновесии в газе все направления скоростей молекул равновероятны. В противном случае это привело бы к образованию направленных макроскопических потоков молекул и возникновению перепадов давления.

Так как скорость и ее проекции являются непрерывными величинами, вводится понятие функции плотности распределения f (v_x), f (v_y), f (v_z) по компонентам скоростей молекул (v_x, v_y, v_z) и по модулю скорости f (v)

.

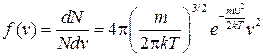Выражения для функций плотности вероятности по компонентам скоростей v_x, v_y, v_z имеют вид

;

.

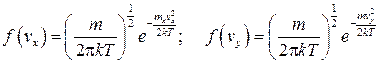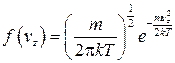График функции f (v_x)изображен на рис. 1.

Функция имеет максимум при v_x = 0, симметрична относительно его и экспоненциально стремится к нулю при v_x ® ± ¥. Отложим по оси абсцисс элементарные скоростные интервалы dv_x около значений v_x, равных 0; ± v_x ¢; ± v_x ¢¢. Произведение f (v_x) dv_x равно доле молекул, компонента скорости v_x которых лежит в интервале около указанных значений. С другой стороны, произведение f (v_x) dv_x на графике равно заштрихованным площадкам около выбранных скоростей.

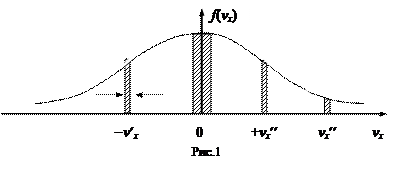Из сопоставления размеров заштрихованных площадей следует:

- относительное большинство молекул имеет проекцию скорости вдоль оси v_x, близкую к нулю;

- доли молекул, имеющих одинаковые значения v_x, но летящие в противоположных направлениях (разные знаки + v_x и - v_x), одинаковы;

- число молекул, имеющих большие значения компонент скоростей, мало (мала площадь около ± v_x ¢¢).

Аналогичный анализ можно провести и для f (v_y), f (v_z).

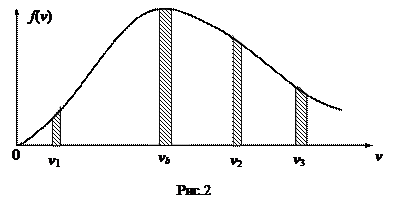График функции f (v) изображен на рис. 2.

Функция равна 0 при v = 0; стремится к нулю при v ® ¥, при v = v_b имеет максимум. Значение скорости v_b, при которой функция плотности распределения достигает максимума, называется наиболее вероятной скоростью. Ее значение находится из условия экстремума.

.

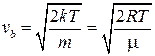Произведение f (v) dv дает долю молекул, скорости которых лежат в выбранном интервале dv. На графике это произведение равно заштрихованным площадкам. Как видно из графика, максимальная площадка соответствует скорости v_b. С увеличением скорости доля молекул, обладающих большими скоростями, уменьшается (малая площадь при v ₃). Зная аналитический вид f (v), можно найти < v >

;

.

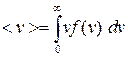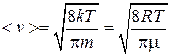Распределение молекул по скоростям зависит от температуры.

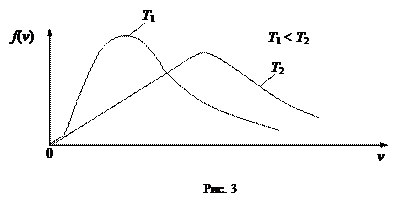На рис. 3 приведены кривые распределения молекул по скоростям при разных температурах. При повышении температуры наиболее вероятная скорость увеличивается, поэтому максимум кривой смещается в сторону больших скоростей. Площади, ограниченные кривыми и осью скоростей, равны единице и не могут измениться при повышении температуры. Вследствие этого максимум понижается по мере повышения температуры и становится менее острым.

Закон Максвелла распределения молекул газа по скоростям описывает поведение очень большого числа частиц, то есть является статистическим законом. Распределение молекул по скоростям устанавливается посредством их столкновений. При столкновениях изменяются скорости отдельных молекул, но закон распределения по скоростям не изменяется.

Эту ситуацию можно понять следующим образом. Выделим среди молекул несколько скоростных групп, то есть групп молекул, скорости которых лежат в интервале dv около значений v_x, v_y, v_z и так далее. Количество молекул в этих скоростных группах обозначим, соответственно, через dN ₁, dN ₂, dN ₃ и т.д. При столкновении молекулы изменяют свою скорость и выбывают из своей скоростной группы в другую. Точно такое же количество молекул переходит в эту скоростную группу из других групп, так что в любой момент времени в состоянии теплового равновесия число молекул в каждой скоростной группе неизменно. Итак, за большой промежуток времени молекула, изменяя скорость при столкновениях, «переберет» все значения скоростей от малых до больших.

Date: 2015-09-25; view: 524; Нарушение авторских прав