
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Площадь многоугольника. Теорема существования
|
|
Пусть М- множество всех многоугольников на евклидовой плоскости.
Опр. 1. Говорят, что установлено измерение площадей многоугольников, если определено отображение S: М®R+, такое, что
S1 если F@F/, то S (F)=S (F/).
S2 если F=F1+F2, то S (F)=S (F1)+S (F2) – аддитивность.
S3 S(Р0)=1, где Р0-квадрат, построенный на единичном отрезке как на стороне. Положительное число S(F) называется мерой или площадью многоугольника А, а квадрат Р0- единичным квадратом.
ЗАМЕЧАНИЕ Раз речь идет об евклидовой плоскости, с введенной на ней системой координат, то ясно, что единичный отрезок уже выбран.
Теорема существования. На евклидовой плоскости существует хотя бы одно отображение S: M® R+, удовлетворяющее аксиомам измерениям площадей.
Доказательство. Зададим это отображение явно:
S (F) =  (1),
(1),
ясно, что это отображение М® R+ по Ch3. Осталось проверить выполнение аксиом S1-S3.
S1) Пусть F=F/. $ движение, переводящее F в F/. По теореме о реперах это движение g может быть задано парой соответствующих ортонормированных реперов R и R/, g(R)=R/,g(R)=R/, если MR(x,y), то g(M)R/(x,y). Если Ai(xi,yi), I =1,…,n вершины многогранника F в R, то в репере R/ точки А/i = g(Ai) будут иметь те же координаты (xi,yi), тогда из формулы (1), §4 Þ½[ 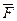 ]½=½[
]½=½[ 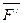 ]½ÞS (F)=S(F/).
]½ÞS (F)=S(F/).
S2) Пусть теперь F=F1+F2. По Ch4, F ориентируем так, чтобы 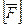 >0. На F1 и F2 введем ориентацию согласованye с
>0. На F1 и F2 введем ориентацию согласованye с 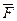 , это можно сделать, т.к. простой многоугольник гомеоморфен сфере с дыркой, а она ориентируема. Получаем
, это можно сделать, т.к. простой многоугольник гомеоморфен сфере с дыркой, а она ориентируема. Получаем 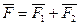 (почему это можно сделать?)
(почему это можно сделать?)
Докажем, что 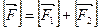 (2).
(2).
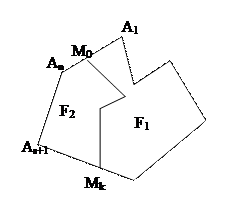
Пусть М0…МК – ломанная, которая разбивает многоугольник F на F1 и F2.  -радиус векторы ее вершин. Вершины многоугольника обозначим так, чтобы А1-М0-Аn и АS –МК-АS+1,
-радиус векторы ее вершин. Вершины многоугольника обозначим так, чтобы А1-М0-Аn и АS –МК-АS+1,  радиус - векторы точек Аi. Тогда
радиус - векторы точек Аi. Тогда
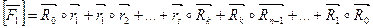

|
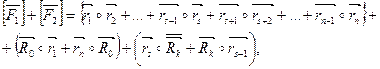 но
но  [Если же М0 совпадает с А1, то
[Если же М0 совпадает с А1, то 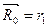 и первая скобка равна
и первая скобка равна 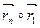 ]
]
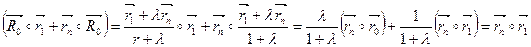
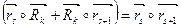 ,
, 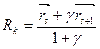 (если Rk совпадает с
(если Rk совпадает с 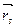 и
и 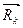 совпадает с
совпадает с 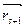 , то сразу). Значит
, то сразу). Значит 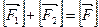
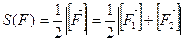 , оба отрицательными быть не могут, т.к.
, оба отрицательными быть не могут, т.к.  >0. Пусть
>0. Пусть 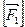 >0, если
>0, если 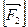 <0, то из (1) получаем
<0, то из (1) получаем  <
< 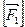 , что противоречит Ch 2.Þ
, что противоречит Ch 2.Þ 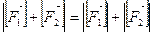 ÞS(F)=S(F1)+S(F2).
ÞS(F)=S(F1)+S(F2).
S3) Пусть Р0 квадрат. Рассмотрим единичный квадрат ОА1А2А3 в системе координат 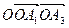 О(0,0), А1(1,0), А2(1,1), А3(0,1).
О(0,0), А1(1,0), А2(1,1), А3(0,1).
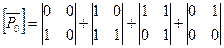 =2ÞS(P0)=1
=2ÞS(P0)=1
Теорема доказана.
Date: 2015-09-24; view: 660; Нарушение авторских прав