Теорема существования

Измерение и длина отрезка

Предположим, что мы находимся в рамках теории, в которой выполняется первые четыре группы аксиом Гильберта, т.е. абсолютная геометрия. Тем самым определено понятие отрезка, равных отрезков и т.д. Под измерением отрезка понимают некий процесс, в результате которого, получается некоторое число. Каждому отрезку ставится в соответствие некоторое положительное число, которое называется его длиной. L- множество всех отрезков, R₊ множество всех действительно положительных чисел.

Опр 1. Будем говорить, что установлено измерение отрезков, если определено отображение l: L® R₊, удовлетворяющим следующим аксиомам:

L1. если отрезки АВ и А^/В^/ равны, то l(АВ)=l(А^/В^/)

L2. если А-В-С, то l(АВ)+l(ВС)=l(АС)

L3. $ отрезок PQ: l(PQ)=1

Отрезок PQ и любой равный ему отрезок называется линейной единицей или единичным отрезком. Положительное число l(АВ) с указанием линейной единицы называется мерой или длиной отрезка АВ.

Постановка задачи: Задача заключается в том, чтобы доказать, что в абсолютной геометрии всегда существует отображение l:L® R₊, удовлетворяющее аксиомам 1,2 и 3, при этом если выбран единичный отрезок PQ, то это отображение определяется единственным образом.

В Á(å_W) это уже сделано. В Á(å_Р) - введено в аксиомы. Сложнее в других теориях. Но во всех этих теориях работает абсолютная геометрия. А после того как докажем единственность, станет ясно, что это та самая длина и есть.

Теорема существования

Теорема (существование длины в абсолютной геометрии). В абсолютной геометрии при любом выборе единичного отрезка PQ существует отображение g: L®R₊, удовлетворяющее трем аксиомам измерения отрезков, причем g (АВ) есть число, полученное в результате измерения отрезка АВ.

Доказательство. Пусть АВ - произвольный отрезок, а PQ – выбранный единичный отрезок. Это типичная Th существования. Мы построим конкретное отображение g, а потом докажем, что оно удовлетворяет L1, L2, L3. Отображение опишем как процесс, ставящий в соответствие каждому отрезку положительное число. Этот процесс и будет называться измерением отрезка. Для доказательства нам понадобится систематические двоичные дроби. Т.е. числа вида, а=n,n₁,n₂,…, где n-целое неотрицательное число, n_i равно 0 или 1. Тогда а= 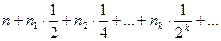. По теореме: Всякое действительное число a можно представить в виде конечной или бесконечной систематической дроби с любым основанием.

1.Построение На луче АВ отложим последовательно отрезки АА₁, А₁А₂,… равные PQ., если А_n совпадает В, то будем считать, что g(АВ)=а=n. Если нет, то $А_n+1:A_n-B-A_n+1- по аксиоме Архимеда. Пусть Р₁- середина отрезка А_nA_n+1. Возможны три случая: а)Р₁- совпадает с В б) А_n-В-Р₁, в)P₁-B-A_n+1. В случае а) будем считать, что g(АВ)=n,1 (a=n+1/2); б) запишем n,0… и) n,1… и перейдем к следующему шагу.

Пусть Р₂ середина того отрезка, который содержит т.B. A_nP₁ (P₁A_n+1). Снова три случая а) Р₂ совпадает с т. В а=n,01или (a=n+ 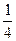)(a=n,11) б) Аn-B-P₂ n,00 n,10… в) P₂-B-P₁ n,01 n,11… и переходим к следующему шагу.

Продолжая этот процесс, приходим к определенному числу а, т.к. каждый раз мы идем по одной ветке и, значит, этот процесс сходится по аксиоме Кантора. g(AB)=a

2. Проверка аксиом L1, L2, L3.

L3- очевидно, т.к. g (РQ)=1

L1. Пусть АB=A^/B^/. Система точек на лучах AB и A^/ B^/,полученная в процессе измерения, имеет одинаковый порядок расположения и отрезки с концами в соответствующих точках равныÞ n=n^/, n^/₁=n₁,…., и g(AB)=g(A^/B^/) (единственность предела)

А вот с L2 сложности.

Лемма 1 Если A^/B^/<АВ, то g(A^/B^/)< g(AB)

Доказательство Отложим на луче АВ отрезок АС равный A^/B^/., т.к. АС<АВ то А-С-В. Т.к. g(A^/B^/) =g(AС) по L1, то будем говорить о g(AС) и g(АВ). G(АС)=n, n₁ n₂… g(AB)=m,m₁ m₂ … если С-А_n-В, то n<m и ч.т.д. Пусть А_n-С-В- А_n+1.Т.к. выбираем середину мы приближаемся к В. Если на к шаге попадем в случай а) процесса, то у В будет 1, а у С 0. всегда на каком-то шаге середина окажется внутри СВ, т.к. половина отрезка меньше целого и значит, выбирая середину меньшего отрезка, мы тем самым уменьшаем отрезок, в котором может содержаться СВ (т.е. получаем бесконечную последовательность вложенных друг в друга отрезков), а больший отрезок в меньшем содержаться, не может. g(AC)<g(AB)ÞЗначит g(A^/B^/)<g(AB) ч.т.д.

Лемма 2 Пусть PQ-единичный отрезок, а ЕF-отрезок, в котором 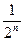-часть отрезка РQ укладывается k раз, где kÎ N. Тогда g(ЕF)= .

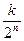Самостоятельно и доказательство L2 тоже.

Доказательство L2:

Пусть А-В-С а= g(AB), в=(ВС), c=g(АС) докажем а + в = с. Пусть çа+в-сç>0 $ n: çа+в-сç>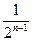

РР_n 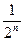часть PQ $A_k+1 и А_к т. что ВА_к£АВ<ВА_к+1, $с_s и с_s+1: BC_s£BC<BC_s+1

Лемма 1Þg(BA_k)£a<g(BA_k+1) g(BC_s) £b<g(BC_s+1) Þ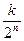

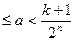
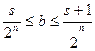
Складываем 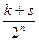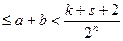A_kC_s £AC< A_k+1C_s+1 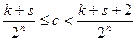на множестве R. ça+b-cç< 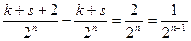противоречие.

Теорема доказана.