Випадкові похибки

В більшості випадків виконується нормальний закон розподілу похибок. Тому за найбільш вірогідне значення вимірюваної величини слід прийняти її середнє арифметичне значення, яке обчислюється із всіх виконаних вимірів. Дуже важливо, щоб усі виміри були виконані з однаковою точністю тобто були рівноточними.

.

Строго, при обчисленні похибок вимірів потрібно користуватись стандартною похибкою – середньою квадратичною похибкою:

.

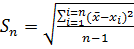Дисперсією називають 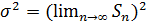. Але часто, виходячи з міркувань зручності використовують середню арифметичну похибку :

(*).

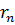Зручність застосування стандартної похибки в якості основного числового виразу похибки спостережень є в тому, що, якщо середня квадратична похибка виражена в долях σ, то можна легко знайти відповідну їй довірчу вірогідність. Для середньої квадратичної похибки, яка дорівнює σ, довірча вірогідність дорівнює 0,68 (тут і далі ми вважаємо, що похибки розподілені по нормальному закону). Середній квадратичній похибці 2σ відповідає довірча вірогідність 0,95, середній квадратичній похибці 3σ відповідає довірча вірогідність 0,997. Обчислення довірчої вірогідності для інших значень похибки виходить за межі даної роботи.

Все це справедливо для досить великої кількості вимірів (n>30). Для малої кількості вимірів краще користуватись формулою не (*), а такою

(**).

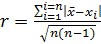Але якщо похибки вимірювань є малими в порівнянні з величиною, яку ми вимірюємо, не має значення якою формулою користуватись (*) чи (**). Тож в школі краще (*), бо простішає процес обчислень.

Нехай вимірювана величина Z є сумою (різницею) величин X та Y (Z=X ± Y), середні квадратичні похибки яких 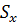та 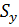, відповідно. Тоді середня квадратична похибка Z:

.

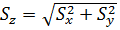Треба пам’ятати, що які б ми похибки не використовували треба складати похибки тільки так. Звідси витікає, що для підвищення точності величини Z (зменшення похибки 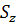) треба зменшувати більшу з похибок 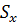і 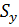. Наведемо ще твердження без доказів:

Середня квадратична похибка середнього арифметичного дорівнює середній квадратичній похибці окремого результату, розділеній на квадратний корінь із кількості вимірювань: .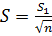

Це означає, що для підвищення точності вимірів (зменшення похибки) у 2 рази, потрібно збільшити кількість вимірів в 4 рази, для підвищення точності вимірів у 3 рази, потрібно збільшити кількість вимірів в 9 разів і т.д. Для школи це має важливе значення, бо деякі з авторів рекомендують повторювати вимірювання 3 ‒ 5 разів. Що дає проти двох вимірювань зменшення похибки у 1,2 - 1,6 разів. Для школи це підвищення точності не має особливого значення, а витрати часу значно збільшуються. Тому ми не бачимо особливого сенсу в великій кількості вимірювань. Для ілюстрування методу досить двох вимірювань, що вчителі мають брати до уваги.

Взагалі збільшувати кількість вимірів має сенс доки випадкова похибка не стане меншою від систематичної. Нехай систематична помилка, яка визначається класом точності приладу, буде δ. Як правило, нема необхідності визначати загальну похибку точніше ніж 10%. Це означає, що достатньо 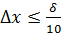. Дуже часто достатньо .

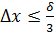Похибки при непрямих вимірюваннях.

Якщо маємо залежність 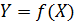, то абсолютну похибку можна записати у вигляді

Відносна похибка матиме вигляд

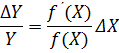
Цей спосіб обчислення відноситься як до випадкових так і до систематичних похибок. Якщо при непрямих вимірах маємо, що Y це функція декількох змінних величин 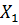, , 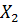,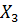…, , 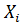то середня квадратична помилка буде дорівнювати

Середня арифметична похибка обчислюється за такою формулою

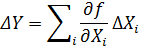
Наведемо деякі приклади обчислення середньої арифметичної похибки для непрямих вимірів (систематична похибка більше випадкової). Зведемо все це в таблицю. В таблиці 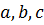- наближені числа; – відповідні їм граничні похибки; 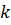- число, константа, коефіцієнт пропорційності.

Таблиця 1

№ з/п	Алгебраїчний вираз (Y)	Абсолютна похибка (ΔY)	Відносна похибка ()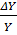

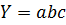
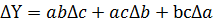
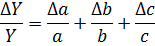
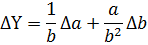
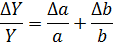
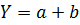
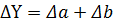
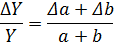
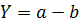
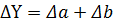
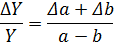
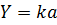
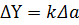
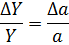
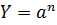
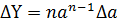
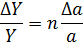
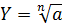
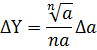
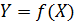
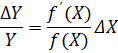
Такі ситуації виникають при визначенні об’єму тіла за допомогою мензурки, або об’єму паралелепіпеду за допомогою лінійки. Аналогічна ситуація виникає в школі при виконанні лабораторних робот з електрики.

Але, наприклад, в лабораторних роботах з оптики випадкова похибка більша систематичної. Тому виникає питання, як обчислювати середнє арифметичне значення і похибку непрямих вимірювань у цьому випадку. Якщо 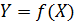і вимірювання дають ряд значень величин 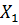, , 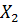,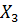…, 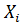. То можна поступати двома способами:

1. обчислити середнє арифметичне значення 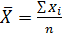. Знаючи обчислити середнє значення 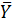за формулою ;

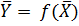2. для кожного значення обчислити 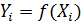, потім обчислити 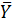за формулою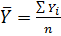

відповідно двома способами можна обчислити похибку величини 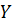, або визначивши похибку 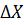величини за формулою 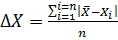і скористуватись формулою 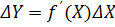. Або, для способу 2, знаючи 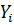, скористатись формулою .

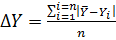Якщо похибки вимірювань малі у порівнянні з вимірюваною величиною (саме це припущення лежить в основі всіх формул), то обидва способи дають практично співпадаючі результати і не має значення яким з них користуватись. Поясним це на прикладі обчислення питомої густини матеріалу, з якого зроблено паралелепіпед. Маса паралелепіпеду – m, об’єм - 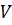, довжини ребер його - 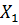, , 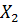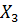. Питома густина визначається з формулою 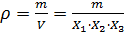. Тоді відносна похибка згідно п.8 таблиці: 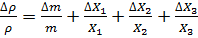. Нехай об’єм тіла 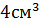. Припустимо, визначення маси відбувається на аналітичних терезах, які дають точність при масі зразка . 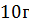Тоді маємо 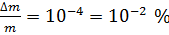. До речі, точність цьому випадку 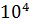Якщо ми бажаємо, щоб точність вимірювання густини визначалась точністю визначення маси, то необхідно, щоб похибка в вимірюванні довжини ребер була менше похибки зважування, тобто 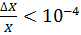; це при розмірі ребер в 1см (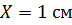) означає, що . Тобто, високоточні вимірювання ребер мають сенс тільки при прецизійному виготовленні тіла. Якщо в нашому розпорядженні є мікрометр, яке дає точність 0,01 мм, що у 10 разів гірше ніж потрібно, то ми маємо зважувати тіло на звичайних технічних терезах. Інакше вимірювання становляться дуже трудомісткими і не досить дешевими. Більшість інструментів, які застосовуються для вимірювання довжини, дають абсолютну похибку, яка, в межах вимірювання, не залежить від довжини ребра тіла. Припустимо, як на рисунку1, що 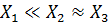. Це означає, що №1) . Тобто, визначаючою похибкою буде похибка самої малої грані. Практично, якщо одна грань в 3 – 4 рази менша від інших, то похибками вимірювання останніх можна нехтувати. Для вчителя: похибка визначення об’єму паралелепіпедів з набору (приблизно такі, як на рисунку) визначається похибкою вимірювання найменшого ребра. Якщо використовуються бруски набору для вимірювання коефіцієнта тертя, то похибка визначення об’єму визначатиметься похибками вимірювань двох коротких ребер. Треба розуміти, 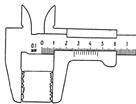що застосування високоточних приладів не завжди обґрунтовано але завжди дорого (див. рисунок №2). Якщо розміри нерівностей перевищують абсолютні похибки приладу, то який сенс в його застосуванні. Дешевше вимірювати звичайною лінійкою. Для визначення об’єму куба з точністю 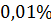без поправок на відхилення кутів від 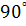, треба щоб ці кути були виготовлені з точністю до кутової хвилини, що дуже складно і тому дуже дорого. Тобто при вимірювання потрібно заздалегідь оцінити можливі похибки і обрати розумні засоби вимірювань.

Окремо декілька слів про похибки при вимірюваннях сили струму і напруги. Похибка при вимірюваннях струму або напруги приладами з покажчиком (стрілкою) визначається за формулою , де 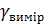– відносна похибка конкретного виміру (в тих же одиницях, що і 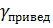); 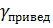– клас точності приладу (на електричних приладах позначка у відносних одиницях); 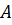– верхня межа вимірів приладу; 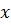– результат конкретного виміру. Клас точності шкільних приладів 4. Це означає, що мінімальна приведена помилка для шкільних приладів дорівнює 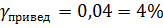. 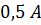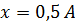Звідси, при вимірюваннях сили струму шкільним амперметром (, ) при силі струму () маємо похибку 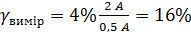. Якщо використовується цифровий прилад, то похибка вказана в паспорті цього приладу, якщо цього нема, то похибкою вважають половину останнього розряду на табло.

Окремо потрібно сказати про лабораторні роботи типу "Дослідження одного з ізопроцесів." (10 кл), "Вивчення теплового балансу за змішування води різної температури.(9кл)". Припустимо в роботі "Вивчення теплового балансу при змішуванні води різної температури" учні отримують результати 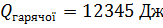і 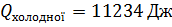. Потім учні пишуть 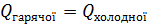і стверджують, що тепловий баланс виконується, чи ще щось у цьому дусі. Тут вчитель повинен застерегти від цього безглуздя і сказати, що потрібно написати щось на кшталт "ми перевірили виконання рівняння теплового балансу з точністю 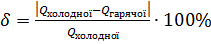". Ідеально було б, якщо б учні навели самостійно, хоча б деякі чинники розходження результатів, не забуваючи, що кожне з цих чисел, і і , визначено з похибкою.

Date: 2015-09-24; view: 1244; Нарушение авторских прав