Функції, обчислювані за реальний час

Нехай маємо строго зростаючу функцію 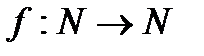- обчислювана за реальний час (RTF) якщо існує машина Тьюрінга А, що має скінчену кількість робочих стрічок, вихідну стрічку та за реальний час генерує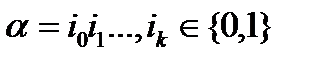 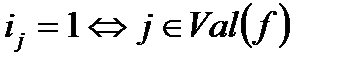(множина всіх значень функції f)

Той факт, що машина А генерує нескінченну послідовність α_f за реальний час означає, що: в початковий момент часу МТ А має порожні робочі стрічки і порожню вихідну стрічку. Потім, на кожному такті роботи МТ А здійснює дії відносно робочих стрічок (зміна символу, що розглядається; зсуви робочих стрічок відносно керуючої голівки; зміна стану керуючої голівки) і друкує лише 1-ин символ на вихідну стрічку.

Функція 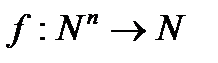називається обчислюваною за реальний час (за допомогою МТ А, що має n вхідних стрічок, скінченну кількість робочих і вих.), якщо для довільних натуральних чисел x_i 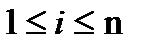вона обчислює значення 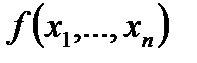за кількість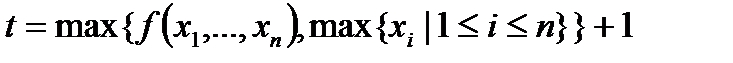

Відносно класу RTF можна довести, що він замкнутий відносно операцій додавання, множення, віднімання (при певних обмеженнях), суперпозиції, піднесення до степеня і т.д.

Доведемо твердження про замкненість відносно операції сумування.

Теорема. Клас функцій, обчислюваних за реальний час, замкнутий відносно операції сумування. Тобто, якщ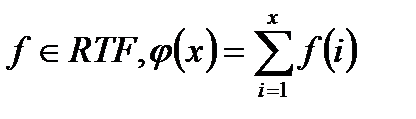о, то .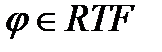

Доведення.

Нехай є машина A_f, яка обчислює за реальний час функцію f. Побудуємо A_ϕ, яка обчислює за реальний час функцію ϕ.

Етап 0. ϕ(0) = 0

Етап x..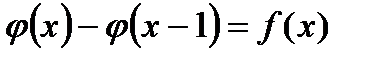

Машина A_ϕ має 1-у додаткову робочу стрічку.

Там вже знаходиться блок довжиною f(x-1). Вказівник рухається по цьому блоку і робить f(x-1) кроків. Потім включається машина A_f. Вона робить f(x)-f(x-1) кроків і паралельно добудовує блок довжиною f(x)-f(x-1).

Здійснюється всього f(x) кроків. На кожному кроці на виході машина A_ϕ друкує “0”, і кінці “1”. Тоді в кінці етапу x в пам’яті буде знаходитись блок довжиною f(x).

Date: 2015-09-24; view: 439; Нарушение авторских прав