Лемма о замещениях

Пусть есть МТ А=<K, Г, l, Н, q₀, q^*> и разметки ленты m₁ и m₂. Пусть на разметке m_i возникает полное поведение q_i, i=1,2 MT A.

Пусть теперь для некоторых i и j (i<j) верно S(i, q₁)=S(j, q₂). След S(i, q_i) конечен, и если q₁=(m₁, q₁, i₁) 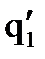, q₂=(m₂, q₂, i₂) , то (i₁<i) & (i₂<j) или (i_1³i) & (i_2³j). Тогда на разметке:

Возникает полное поведение q₃ МТ А такое, что "k

Доказательство будем вести индукцией по n – длине следа S=S(i, q₁), n=|S|.

При n=0 в случае (i₁<i) & (i₂<j) имеем, что начиная с разметки m₁ МТ не заходит правее (i-1)-ой ячейки, а тогда "k ³i |S(k, q₁)|=0. Аналогично, "k ³j |S(k, q₂)|=0, а тогда утверждение леммы тривиально. Случай (i₁³i) & (i₂³j) разбирается аналогично. Пусть мы доказали лемму для некоторого n. Докажем ее справедливость для n+1. Пусть (i₁<i) & (i₂<j). Поведение q₁ и q₂ можно представить в виде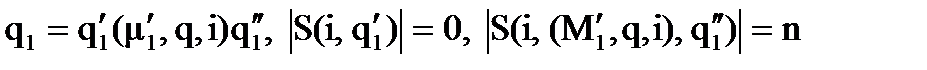

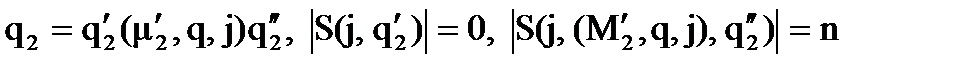
Остаточные поведения 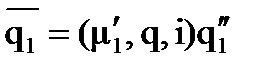и являются полными, и их следы на i-m и j-m разрезах соответственно совпадают и меют длину n, к тому же (i=i) & (j=j). Мы попадаем в условия леммы, а тогда на разметке возникает полное поведение МТ А такое, что "k

Заметим, что .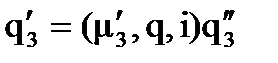

Поведение q₃ на разметке m₃ можно представить в виде

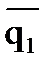получено из 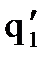заменой разметки m на такую

Имеем:

Что и требовалось доказать.

Случай (i₁³i) & (i₂³j) разбирается аналогично. По принципу мат. индукции лемма доказана.

Date: 2015-09-24; view: 418; Нарушение авторских прав