Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Функції складності (сигналізуючі) за часом та за пам’яттю. Теорема про прискорення
|
|
В теорії складності обчислень розглядаються обчислювальні задачі чи задачі розпізнавання (аналізу) і досліджуються питання складності розв’язку цих задач на відповідних обчислювальних пристроях. Основний інтерес представляє отримання оцінок складності задач по часу і по пам’яті. Відповідно при розгляді обчислень на машинах Тьюрінга вводяться поняття часової сигналізуючої і сигналізуючої по пам’яті.
Нехай A=(K,Σ, A`, H, q0, q*)- машина Тьюрінга, що розпізнає мову L(A), де L(A)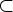 
Σ*. Вважається, що при довільному вхідному слові w є Σ* машина Тьюрінга A, розпочавши роботу в конфігурації q0w, зупиниться через скінченну кількість кроків (через tA(w) кроків) і при цьому вона використає lA(w) комірок робочої стрічки.
При цьому якщо вона зупиниться в кінцевому стані q*, то маємо, що w є Σ*, а в іншому випадку, маємо, що Σ ∉ w. Тепер визначимо для машини Тьюрінга A часову сигналізуючу TA(x) і сигналізуючи по пам’яті LA(x).
Покладемо, що
TA(x)=max{tA(w)|wє Σ*, |w|<=x}
LA(x)=max{tA(w)|wє Σ*, |w|<=x}
Будемо говорити, що задача розпізнавання w є Σ* має верхню (часову) оцінку (в.о.) T(x), якщо існує машина Тьюрінга A, що розпізнає мову L і TA(x) <= T(x)для всіх натуральних чисел x.
Будемо говорити, що задача розпізнавання w є Σ*має нижню (часову) оцінку (н.о.) T(x), якщо доведено, що для довільної машини Тьюрінга A, що розпізнає мову L виконується співвідношення T (x) <= TA (x) для всіх натуральних чисел x.
Будемо говорити, що задача розпізнавання w є Σ* має оптимальну (часову) оцінку (о.о.) T(x), якщо функція T(x) є одночасно н.о. і в.о. для цієї задачі.
Теорема про прискорення. Нехай деяка задача розв’язується на МТ A з часовою сигналізуючою TA (x), де TA (x) ≥ x2. Нехай c - довільне натуральне число і c ≥ 2. Тоді існує МТ B, яка розв’язує ту ж задачу з часовою сигналізуючою TB(x), де TB(x) <= 1/c TA(x) для майже всіх x.
Доведення. Ідея доведення полягає в укрупненні комірок.
Нижня квадратична оцінка тут важлива, бо на перебудову слова в алфавіті Σ потрібний квадратичний час, якщо Σ≥|2|.
Якщо ж вхідні і вихідні слова представлені в однобуквеному алфавіті, то в формулюванні теореми замість нижньої оцінки x2 можна взяти оцінку xlog x.
Date: 2015-09-24; view: 403; Нарушение авторских прав