
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Контролирующий блок
|
|
Тема «Функции одной переменной»
Тест 1.
1. Какие из следующих зависимостей не будут функциональными?
А. Каждому числу соответствует квадрат этого числа;
В. Каждому числу, не равному нулю, соответствует квадрат этого числа;
С. Каждому числу соответствует противоположное ему число;
D. Каждому неотрицательному числу соответствует корень квадратный из этого числа;
Е. Все зависимости функциональные.
2. Найти область определения функции 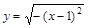 .
.
А. [1;+∞); В. (-∞; 1]; С. {1}; D. (-∞;+∞); Е. Ø.
3. Множество значений функции 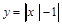 есть промежуток…
есть промежуток…
А. (0; +∞); В. (1; +∞); С. (-∞; 0);
D.(-∞; +∞); Е. [0; +∞).
4. С какой из прямых график функции у=f(х) не может пересекаться в нескольких точках?
А. у=а; В. у=k x; С. х=b; D. у=k x + b; Е. Таких прямых нет.
5. При каких значениях k точка А(4;-1) лежит на графике функции у = k 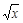 ?
?
А. 4; В. –1; С. ½; D. –½; Е. Ответ отличен от указанных.
6. 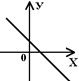
| На рисунке изображен график функции у=а х + в. Укажите знаки а и в. А. а >0, в >0; В. а >0, в <0; С. а <0, в >0; D. а <0, в< 0; Е. а >0, в =0. |
7. Какой из следующих графиков функции может быть графиком функции у=х ² - 6 х + а?
А.  ; В.
; В. 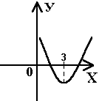 ; С.
; С.  ;
;
D. 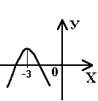 ; Е.
; Е.  .
.
8.На рисунке изображен график функции у= 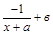 . Укажите знаки а и в. . Укажите знаки а и в.
| 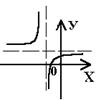
| А. а <0; в >0; В. а >0; в >0; С. а <0; в <0; D. а >0; в <0; Е. Знаки а и в определить нельзя. |
9. Сколько точек графика квадратного трехчлена необходимо знать, чтобы определить его коэффициенты?
А. 2; В. 3; С. 4; D. 5; Е. Нельзя определить коэффициенты по точкам графика функции.
10. Какие из данных функций не являются убывающими?
А. у = -2 х +1; В. у = - 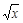 ; С. у = х ², х< 0;
; С. у = х ², х< 0;
D. у = 1/ х, х >0; Е. у= 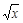 .
.
11. При каких значениях k функция у = k/x будет возрастать на интервале (0;+∞)?
А. При любом k; В. k ÎÆ; С. k ≤0;
D. k <0; Е. k >0.
12. Функция у=f (х) является убывающей. Какая из следующих функций не является убывающей?
А. у=f (х+ 1); В. у= 3 f (х); С. у=f (х) - 2;
D. у=-f (х); Е. у=f (2 х).
13. Какие из следующих функций четные?
А. у=  , х> 0; В. у=х ², х > - 1; С. у=
, х> 0; В. у=х ², х > - 1; С. у= 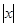 ,-3≤ х ≤4;
,-3≤ х ≤4;
D. у= (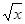 )²; Е. у=х ²,
)²; Е. у=х ², 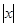 >1.
>1.
14. Функция у=f (х) является нечетной, причем f (2) = 3, f (-1) = 5. В каких еще точках можно указать значения этой функции?
А. –2; 0; В. 1; -2; С. 1; -2; 0; D. –3; -5; Е. Ни в каких.
15. Функция у=ах + в является нечетной при…
А. в <0, а <0; В. а >0, в >0 С. в =0;
D. а >0, в <0; Е. а =0.
16. Функция у=f (х) четная. Какая из следующих функций не является четной?
А. у=f (2 х); В. у=|f (х)|; С. у=f (х)+1;
D. у=f (х- 1); Е. у=f (| х|)
17. Какие из функций обратимы?
А. у=|х|; В. у=  ; С. у=х
; С. у=х
D. у=х ², х ≥0; Е. у=х ², х ≥-1.
18. Известно, что функция у=f (х), х ε[ а; в ] обратима. Какая из следующих функций обязательно необратима?
А. у=f (х)+2; В. у=f (х- 2); С. у=|f (х)|;
D. у=f (| х|); Е. у=f (х/ 2).
19. Функция обратима, если она …
А. Четная; В. Возрастающая; С. Непрерывная;
D. Нечетная; Е. Ограниченная.
20. Если функция f (x) = ln x, g (x) =  , то функция f (g (x)) равна…
, то функция f (g (x)) равна…
А. (½)ln | х- 1|; В.  ;
;
С. (½) ln (х- 1) при х> 1; не определена при х≤ 1; D. (ln х) 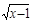 ;
;
Е. Не определена при х εR.
21. Областью определения функции у=h (g (x)), где h (x)= 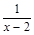 , g (x)=
, g (x)= 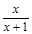 , есть множество…
, есть множество…
А. R\{2;-1}; В. R\{2}; С. R\{-1};
D. R\{-2;-1}; Е. R\{-2;-1;2}.
22. Функция у=f (х) убывающая. Сколько решений имеет уравнение f (х)= а?
А. Одно; В. Ни одного; С. Не более одного; D. Хотя бы одно; Е. Ответ отличен от приведенных.
| 23.График функции у=f (х) изображен на рисунке. Укажите все значения параметра а, при которых уравнение f (х)= а имеет точно одно решение. |
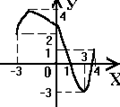
| А. а=- 3, а= 4; В. 1≤ а ≤2; С. -3≤ а ≤4; D. 1< а <2; Е. 1< а <2, а=- 3, а= 4. |
24. Функция у= а х обладает свойством:
А. f (х у)= f (х)+ f (у); В. f (х + у)= f (х)+ f (у);
С. f (х + у)= f (х)∙ f (у); D. f (х у)= f (х)∙ f (у);
Е. Ответ отличен от приведенных.
25. Число π является периодом для функции…
А. у=tg (x/ 2 +π/ 3); В. у=cos 2 x; С. у=sin 2 х, х ε[-100π; 100π]; D. у=sin (x/3); Е. у= 1 /sin πx.
Дополнительные задания по вопросам применения функций в экономическом моделировании:
26. Фиксированные издержки составляют 10 000 руб. в месяц, переменные издержки – 30 руб., выручка – 50 руб. за единицу продукции. Составить функцию прибыли.
А. Р(х) = 20 х -10 000; В. Р(х) = 80 х -10 000; С. Р(х) = 50 х +10 000;
D. Р(х) = 30 х +10 000; Е. Р(х) = 0.
27. Функция издержек производства шин имеет вид С(х)=30 х+ 2100. Цена одной шины 60 руб. Найти точку безубыточности.
А. 0; В. 70; С. 60; D. 30; Е. 2100.
28.

| Потребитель «А» решает, каким образом распределить свой доход между покупкой грампластинок и одежды. На чертеже показаны его бюджетная линия и кривая безразличия. Укажите на данном рисунке точки, в которых «А» максимизирует свои потребности. А. а; В. в; С. с; D. d; Е. f. |
29. Пусть кривая Лоренца, описывающая зависимость процента доходов от процента имеющего их населения, задана функцией у= 1- 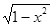 (часть окружности).
(часть окружности).

| Найти коэффициент Джини k=  .
А. π/2-1; В. ½; С. π/4; D. 0; Е. 1. .
А. π/2-1; В. ½; С. π/4; D. 0; Е. 1.
|
30. Производительность некоторого производства с течением времени описывается функцией (эмпирически установленная формула отражает вполне реальный процесс работы) ¦(t) = р 0(-0,2 t 2/ t 02 + 1,6 t/t 0 + 3), где р 0 – размерность производительности (объем продукции в часах), t – время в часах, t 0 – размерность времени (1 час). По графику этой функции опишите процесс работы.
А. Производительность стабильная в течение всего рабочего времени;
В. Производительность монотонно убывает;
С. Производительность монотонно возрастает;
D. Производительность возрастает в первой половине рабочего дня и убывает после четырех часов работы;
Е. Производительность убывает в первой половине рабочего дня и возрастает во второй.
Тема «Предел и непрерывность функции»
Тест 2:
1. Найти общий член последовательности 0, 1/3, 2/4, 3/5, 4/6, …,
А. n/(n+2); В. (n-1)/(n+1); С. (n-1)/(2n-1);
D. (n-2)/n; Е. (n+1)/(n+3).
2. Является ли последовательность с общим членом 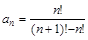
а) монотонной, б) ограниченной, в) сходящейся, г) бесконечно малой, д) бесконечно большой?
А. Только а); В. Только б); С. Только а), б), в);
D. а), б), в), г); Е. Только а), в), д).
Вычислить пределы последовательностей:
3. 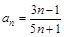 . А. 3/5; В. 0; С. 1; D. ∞; Е. 5/3.
. А. 3/5; В. 0; С. 1; D. ∞; Е. 5/3.
4.  . А. 0; В.1/3; С. 1; D. ∞; Е. 3.
. А. 0; В.1/3; С. 1; D. ∞; Е. 3.
5. 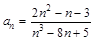 . А. 2; В. 0; С. 1; D. ∞; Е. 1/2.
. А. 2; В. 0; С. 1; D. ∞; Е. 1/2.
6. Какое из условий является достаточным для существования предела функции?
а) равенство односторонних пределов: 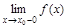 =
=  ;
;
б) существование функции в этой точке;
в) чтобы предел функции в точке 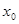 равнялся значению функции f (x) в этой точке.
равнялся значению функции f (x) в этой точке.
А. а); В. б); С. в);
D. Все Е. Ни одно.
Вычислить пределы функций:
7. 
 А. 3; В.1/2; С. –3; D. 1; Е. 0.
А. 3; В.1/2; С. –3; D. 1; Е. 0.
8. 
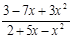 А. –3; В. 0; С. –8; D. 2; Е. ∞.
А. –3; В. 0; С. –8; D. 2; Е. ∞.
9. 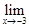
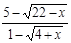 А. 3; В. –3; С. 1; D. -(1/5); Е. 0.
А. 3; В. –3; С. 1; D. -(1/5); Е. 0.
10. 
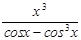 А. 2; В. 0; С. 1; D. –2; Е. –1.
А. 2; В. 0; С. 1; D. –2; Е. –1.
11. 
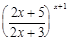 А. е2; В. 1/е; С. е; D. е3; Е. е-2.
А. е2; В. 1/е; С. е; D. е3; Е. е-2.
12. Какое из следующих утверждений является верным:
а) алгебраическая сумма любого конечного числа бесконечно малых функций – функция бесконечно малая;
б) произведение конечного числа бесконечно малых функций есть функция бесконечно малая;
в) произведение бесконечно малой функции на функцию ограниченную есть функция бесконечно малая;
г) если f (x) – бесконечно малая функция, то и 1/ f (x) - бесконечно малая функция.
А. Только а), б); В. Только а), б), в); С. Только в), г); D. Все; Е. Нет верных.
13. Даны бесконечно малые функции при х →0: sin x, tg x, x ², 1-cos² x. Какие из них являются эквивалентными бесконечно малыми функциями?
А. Все; В. Нет; С. Только sin x и tg x; D. Только x ² и 1-cos² x; Е. sin x и tg x; x ² и 1-cos² x.
14. Допишите определение непрерывности функции: функция f (х) называется непрерывной в точке 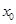 , если…
, если…
1) она определена в этой точке;
2) существует  ;
;
3) предел  равен значению функции в этой точке;
равен значению функции в этой точке;
4) равны односторонние пределы, то есть 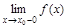 =
=  .
.
А. 1), 2), и 3); В. 4; С. 1), 4); D. 2), 3); Е. 3), 4).
15. Является ли непрерывной функция ¦(х)= 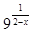 ?
?
А. Да; В. Имеет разрыв I рода; С. Имеет разрыв II рода; D. Имеет устранимый разрыв; Е. Имеет разрывы I,II рода
16. Найти точки разрыва функции 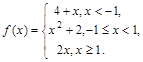
А. х = ±1 разрыв I рода; В. х =±1 разрыв II рода; С. х = -1 разрыв I рода;
D. х =1 разрыв I рода; Е. Нет точек разрыва.
17. Какие из данных функций имеют одну точку разрыва?
А. у=  ; В. у=
; В. у= 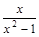 ; С. у=
; С. у= 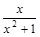 ;
;
D. у=  ; Е. у= | х |.
; Е. у= | х |.
18. Доопределить значение параметров а и в, чтобы функция 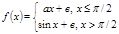 была непрерывной.
была непрерывной.
А. а= 2/p, в= 0; В. а= 1, в ÎR; С. а=в;
D. а, в ÎØ; Е. а= 2/p, в ÎR.
19. Функция у=f (х) непрерывна на промежутке [ а; в ]. Какая из следующих функций может быть разрывной на этом промежутке?
А. у=f³ (х); В. у=f (2 х); С. у=f (х)+1;
D. у= 1 /f² (х); Е. у=|f (х)|.
20. Какое из утверждений верно?
А. Если функция у=f (х)+ g (x) непрерывна, то непрерывны и функции у=f (х) и у=g (х);
В. Если D(f)=(-∞;+∞), то функция у=f (х) непрерывна;
С. Сумма двух непрерывных функций есть функция непрерывная;
D. Частное от деления двух непрерывных функций есть функция непрерывная;
Е. Если функция у=f (х) непрерывна, то у= 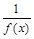 непрерывна.
непрерывна.
21. Функция у=f (х) непрерывна на промежутке [ а; в ] и f (а) f (в)<0. Сколько нулей имеет она на этом промежутке?
А. 1; В. Не более двух; С. Не более одного; D. Не менее одного; Е. Ответ отличен от приведенных.
22. Дописать предложение: функция, непрерывная на отрезке [ а, в ], …
а) достигает на этом отрезке своего наибольшего и наименьшего значений больше одного раза;
б) по меньшей мере, один раз достигает на этом отрезке своего наибольшего и наименьшего значений;
в) не достигает своего наибольшего и наименьшего значений;
г) достигает нуля в некоторой точке этого отрезка;
д) ограничена на этом отрезке.
А. а), д); В. б), д); С. в), г);
D. г), д); Е. нет верных.
23. Какими положениями можно руководствоваться при отыскании точек разрыва функции:
а) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной во всех точках какого-либо интервала;
б) элементарная функция может иметь разрыв только в той точке, где она не определена, при условии, если она будет определена хотя бы с одной стороны от этой точки в сколь угодно близких к ней точках;
в) неэлементарная функция может иметь разрывы как в точках, где она не определена, так и в точках, где она определена;
г) если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов изменения аргумента, то она может иметь разрывы в тех точках, где меняется ее аналитическое выражение.
А. Только а), б); В. Только б), в); С. Только в), г); D. Ни какими; Е. Всеми.
24. Первоначальный депозит Qo помещен в банк под p= 100% годовых. Доход, который можно получить при непрерывном начислении процентов, может составить за год не более чем …
А. 100%; В. (е -1)100%; С. 2,71 Qo; D. 2 Qo; Е. Qo.
25. Пусть темп инфляции составляет 1% в день. Как изменится первоначальная сумма через полгода?
А. Qe1.82; В. Q/e1.82; С. Qе0.5; D. Q/е0.5; Е. Q/2.
Литература
1. Ведина О. И., Десницкая В. Н., Варфоломеева Г. Б., Тарасюк А. Ф. Математика. Математический анализ для экономистов. Учебник / Под ред. А. А. Гриба и А. Ф. Тарасюка – М.: Информационно-издательский дом «Филинч», Рилант, 2006.
2. Выгодский М.Я. Справочник по высшей математике (для вузов и втузов). – М.: 2005.
3. Ермаков В. И. и др. Общий курс высшей математики для экономистов. Учебник / Под ред. В. И. Ермакова – М.: ИНФРА – М, 2001.
4. Ермаков В. И. и др. Сборник задач по высшей математике для экономистов. Учебник / Под ред. В. И. Ермакова – М.: ИНФРА – М, 2001
5. Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании. Учеб. – 2-е издание испр. – М.: Дело, 2001.
6. Кремер Н.Ш. и др. Высшая математика для экономистов / Под ред. Н. Ш. Кремера, - М.: ЮНИТИ, 2005.
7. Кремер Н.Ш. и др. Практикум по высшей математике для экономистов / Под ред. Н. Ш. Кремера, - М.: ЮНИТИ, 2005.
8. Кузнецов А. В. и др. Сборник задач и упражнений по высшей математике: Общий курс: Учебное пособие / А.В. Кузнецов, Д. С. Кузнецов, Е. И. Шилкина и др. – Мн.: Высшая школа, 2001.
9. Миселимян Т. Л. Тренировочные тесты по математике. Ч 1, 2. Уч.-мет. пособ. Кр-р. 2006.
10. Миселимян Т. Л. Функции одной переменной. Теория пределов. Модуль 2. Уч.-мет. пособ. Краснодар. 2007.
11. Солодовников А. С., Бабайцев В. А., Бранков А. В., Шандра И.Г. Математика в экономике.Учеб. – 2-е издание перераб. и доп., Ч.1– М.: Финансы и статистика, 2006.
12. Солодовников А. С., Бабайцев В. А., Бранков А. В., Шандра И.Г. Математика в экономике.Учеб. – 2-е издание перераб. и доп., Ч.2– М.: Финансы и статистика, 2005.
13. Шипачев В.С. Высшая математика. Учеб. – 7-е издание, стер. – М.: Высшая школа, 2005.
Учебное издание
Date: 2015-09-24; view: 492; Нарушение авторских прав