Обучающий блок

Содержание лекций (тезисы)

Лекции 1.1, 1.2: «Функции одной переменной»

Вопросы:

1.Понятие множества.

2.Определение функции, основные свойства.

3. Основные элементарные функции.

4.Классификация элементарных функций.

Понятие множества: Множество – одно из фундаментальных понятий математики. Синонимы: система, совокупность, группа, семейство,… Множество можно определить как совокупность объектов, объединенных по определенному признаку. Объекты множества – элементы множества.

Обозначение: А, В, С - множества, а, в, с, -элементы множества. аεА – «а принадлежит множеству А». Ø – пустое множество.

Задание множества: перечислить его элементы, например, А={1,2,3}, определить правило принадлежности элемента множеству, что соответствует записи А= {a| правило}.

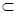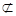Соотношения между множествами: А=В, А В, А В.

Операции над множествами: 1) А+В (или объединением А 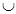В) – множество, состоящее из элементов множества А и множества В, т.е. А 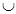В={х│хεА или хεВ}. Геометрическая иллюстрация.

Пример: А+ Ø=А.

2) АВ (или пересечением А В) называется совокупность элементов, входящих как в А, так и в В, т.е. А В={х│хεА и хεВ}. Геометрическая иллюстрация. Пример: А Ø= Ø, А В = Ø то А и В не пересекаются.

3) Разностью А\В называется множество, состоящее из всех элементов А, не содержащихся в В, т.е. А\В={х│хεА и х В}. Геометрическая иллюстрация. Пример: А- Ø=А.

Числовые множества: N, Z, Q, R, C – комплексные, т.е. С={z│z=a+bi, aεR, bεR, i²=-1}. Свойства операций над вещественными числами. (Повторить самостоятельно.)

Числовая прямая и множества на ней: Между А и В установлено соответствие, если по какому-либо закону или правилу любому элементу а из А соответствует элемент в из В. Соответствие называется взаимно однозначным, если 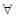аεА соответствует только один элемент из В, и наоборот. Между R и множеством точек на прямой установлено взаимно однозначное соответствие. Числовые множества: [a, b] – отрезок, (a, b) – интервал, (a, b],: [a, b) – полуинтервалы, (-∞, b], [a, +∞),(-∞, +∞) – множество R.

ε- окрестность точки с координатой а: О_ε(а)=(а-ε, а+ε). Точка аεА называется внутренней точкой этого множества, если О_ε(а) 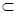А, граничной точкой, если в любой окрестности а содержатся как точки, принадлежащие А, так и не принадлежащие А.

Определение функции: Постоянной величиной называется величина, сохраняющая одно и то же значение. Пример. Отношение длины окружности к ее диаметру есть постоянная величина, равная числу p @ 3,14. Если величина сохраняет постоянное значение лишь в условиях данного процесса, то она называется параметром. Переменной называется величина, которая может принимать различные числовые значения.

Определение. Если каждому элементу х множества Х (хÎ Х) ставится в соответствие вполне определенный элемент у множества Y (уÎY), то говорят, что на множестве Х задана функция у = f (х). При этом х – независимая переменная (аргумент), у – зависимая переменная (функция), f – означает закон соответствия.

Множество Х называется областью определения (существования)функции, а множество Y – областью значений функции.

Если множество Х специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной х, т.е. множество таких значений х, при которых функция у = f (х) вообще имеет смысл.

Способы задания функций: 1.Аналитический (формулы). 2.Табличный. 3.Графический. 4.Словесный (описание правилом).

Основные свойства функций. 1) Четность и нечетность. Четная, если f (-х) = f (х) и нечетная, если f (-х) = - f (х). В противном случае ф-ция у = f (х) не является ни четной ни нечетной.

2) Монотонность. Пусть х₁,х₂ÎХ и х₂>х₁.Þ Функция у = f (х) возрастает, если f (х₂)> f (х₁), и убывает, если f (х₂) < f (х₁).

3) Ограниченность. Если существует М>0, что │f (х)│≤ М для любых х.

4) Периодичность. Если f (х + Т) = f (х), Т≠0.

Основные элементарные функции:

- степенная у=хⁿ, nεN, у=х^-n, nεN, у= 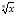, nεN,

- показательная у=а^х, а>0, a≠1,

- логарифмическая у=log_ax, а>0, a≠1,

- тригонометрические у=sinx, cosx, tgx, ctgx,

- обратные тригонометрические y= arcsinx, arccosx, arctgx, arcctgx.

Явное задание: у=f(x), неявное задание F(x, y)=0.

Взаимно-однозначная функция, если для любых х₁, х₂ и х₁ ≠ х₂ выполняется f(x₁)≠f(x₂).

Пусть у=f(x) взаимно-однозначная функция => х=φ(у) или у= φ(х) или у=f ^-1(x) – обратная по отношению к данной.

Теорема. Если у=f(x) строго монотонная на множестве Х, У – множество ее значений, тогда: 1) у=f(x) – взаимно однозначная на Х, следовательно существует обратная f ^-1(x) на множестве У; 2) f (x) и f ^-1(x) возрастают (строго) одновременно (убывают строго).Доказательство самостоятельно.

Сложная функция: Пусть функция у = f(и) определена на множестве и. У – область изменения. и= φ(х) определена на множестве Х. И – ее область изменения. Тогда у = f(φ(x)) (сложная функция) определена на множестве Х.

Определение: Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Классификация функций.

- Алгебраические (целая рациональная функция, дробно-рациональная, иррациональная)

- Трансцендентные (показательная, логарифмическая, тригонометрические, обратно тригонометрические).

Преобразование графиков: С помощью графика функции y = f(x) построить график функции y= m f (k(x + a)) + b.

Применение функций в экономике.

1. Функции Л. Торнквиста – зависимость спроса на различные товары от дохода 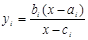, х>а_i i=1,2,3.

2. Кривые спроса и предложения (паутинообразная модель)

3. Кривые безразличия – линии, вдоль которых полезность двух благ х и у одна и та же. xу=U

Линия бюджетного ограничения р_х + р_уу= I, р_х, р_у –цены, I- доход потребителя. х₀,у₀ -оптимальные количества благ, имеющих max полезность U₀.

4. Рассматривая функции издержек С(q) и дохода r(q) фирмы, можно установить зависимость прибыли φ(q)= С(q) - r(q).

Задание функций в виде таблиц Нахождение неизвестных приближенных значений функций по известным ее значениям в заданных точках называется интерполированием (интерполяция). Экстраполяция. Линейная интерполяция. 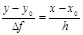=> у=у₀+Δf 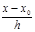(второе слагаемое – интерполяционная поправка).

Лекция 1.3: «Предел и непрерывность»

Вопросы:

1. Предел числовой последовательности.

2.Первый и второй замечательные пределы

Предел последовательности.

Определение. Если по некоторому закону каждому числу nєN поставлено в соответствие вполне определенное число а_n, то говорят, что задана последовательность {а_n} =a_1, a₂, …a_n, … а_n- общий член последовательности.

Определение. а – предел {x_n} ó 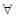ε > 0 N(ε) | |x_n-a|< ε при n>N (ε).

Геометрическое толкование предела: ε фиксируем => N(ε), начиная с которого а_N=1, a_N+2,…принадлежат O _ε(a).

Теоремы о сходящихся последовательностях. Последовательность, имеющая предел, называется сходящейся.

Т1. Сходящаяся последовательность имеет только один предел.

Т2. Сходящаяся последовательность ограничена.

Основные теоремы о пределах последовательностей. Пусть х_n→a, y_n→b при n→∞. Тогда 1) х_n± y_n→ a±b, 2) х_n y_n→аb, (следствие – константу можно выносить за знак предела), 3) х_n/ y_n→а/b. Примеры.

Теорема. Если числовая последовательность монотонна и ограничена, то она имеет предел.

Первый замечательный предел: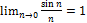

Второй замечательный предел: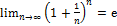

Лекция 1.4: «Предел и непрерывность»

Вопросы:

1.Предел функции в бесконечности и точке.

2.Сравнение бесконечно малых.

Предел функции в точке. Пусть у= f(x) задана в окрестности точки х₀, кроме быть может в самой точке х₀.

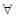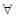Определение. Число А называется пределом функции f(x) ó ε > 0 δ(ε) | | f(x) - A| < ε при |х-х₀| < δ(ε) x ≠ x₀.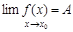

Геометрический смысл. Пример 1) 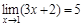, 2) 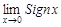не существует.

Замечание. Наличие или отсутствие предела определяется поведением функции в окрестности точки (т.е. существование функции в самой точке не требуется).

Предел функции в бесконечности

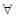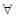Определение. А – предел функции f(x) при х→∞ ó ε > 0 М(ε) | | f(x) - A| < ε при |х| > М(ε) x ≠ x₀. .

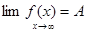Основные теоремы о пределах.

1) f(x) →Ạ, v(x) →B при х→х₀ (х→∞) => 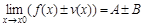; ; 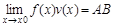, В≠0

2) Функция не может иметь более одного предела;

3) f(x)≤z(x)≤v(x), f(x) →Ạ, v(x) →А при х→х₀ (х→∞) =>z(x)→A при х→х₀ (х→∞);

4) у=f(v(x)), v(x) →U₀ при х→х₀ , f(U)→A при u→u₀=> ;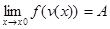

5) f(x) →Ạ, v(x) →B при х→х₀ (х→∞) и f(x) < v(x) в О(х₀) => А<В.

Бесконечно малые величины. Отношения б/м. Свойства б/м.

Бесконечно большие величины. Свойства б/б. Связь между б/м и б/б величинами.

Формула сложных процентов. Q_n= Q₀(1+p/100)ⁿ, где р- процентная ставка за определенный период времени, n- количество периодов хранения вклада. Непрерывное начисление процентов.

Лекция 1.5: «Предел и непрерывность»

Вопросы:

1.Непрерывность функции в точке.

2.Точки разрыва функции.

Определение. Говорят, что функция f(х), определенная в точке х₀ и ее окрестности, непрерывна в точке х₀, если .

Определение. Пусть f(x) определена в точке х₀ и ее окрестности. ∆х=х-х₀ – приращение аргумента, ∆f= f(x₀+∆х) – f(x₀) – приращение функции. Функция называется непрерывной в точке х₀, если 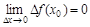, т.е. бесконечно малому приращению аргумента соответствует б/м приращение функции.

Определение. Функция f(х), определенная в точке х₀ и ее окрестности, непрерывна в точке х₀, если 1) существуют конечные односторонние пределы функции в точке х₀ 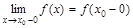и 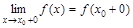; 2) равны между собой 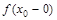= 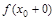; 3) и равны значению функции в этой точке = = .

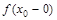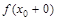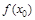Определение. Говорят, что функция f(х) непрерывна на (а,в), если она непрерывна в каждой точке этого интервала.

Говорят, что функция f(х) непрерывна на [а,в], если она непрерывна в каждой точке этого интервала и непрерывна справа в точке а и непрерывна слева в точке в.

Непрерывность функции в данной точке выражается непрерывностью ее графика при прохождении данной точки.

Точки, в которых функция не является непрерывной, называются точками разрыва функции. Примеры.

Свойства функций, непрерывных в точке:

1. Если f(x) и v(x) непрерывны в точке х₀, то f(x) ± v(x), f(x) ·v(x), f(x) / v(x) при условии, что v(x₀)≠0, являются функциями, непрерывными в точке х₀. Доказательство следует из определения непрерывности и аналогичных свойств пределов функции.

2. Если f(u) непрерывны в точке u₀, а u=v(x) непрерывна в точке х₀, то сложная функция у=f(v(x)) непрерывна в точке х₀.

3. Если у=f(x) непрерывна в точке х₀ и f(x₀)>0, то существует окрестность точки х₀ такая, что для любой точки х из этой окрестности выполняется неравенство f(x)>0.

4. Всякая элементарная функция непрерывна в области ее определения.

Замечание: Непрерывность функции в области определения гарантируется лишь для элементарных функций. Для неэлементарных функций гарантии такой нет. Пример. f(x)=[x] («антье» х – целая часть числа).

Свойства функций непрерывных на [a, b].

1-я теорема Вейерштрасса. Если функция непрерывна на отрезке, то она ограничена на этом отрезке. Доказательство от противного.

2-я теорема Вейерштрасса. Непрерывная на отрезке функция достигает на этом отрезке наибольшее и наименьшее значения.

Теорема Больцано-Коши. Пусть функция у=f(x) определена и непрерывна на [a, b] и на концах этого отрезка принимает значения разных знаков f(a)f(b)<0. Тогда существует такая точка c, принадлежащая этому отрезку, в которой функция f(c)=0. Доказательство.

Теорема 4. Пусть функция у=f(x) определена и непрерывна на [a, b] и f(a) ≠ f(b). Для любого числа L, f(a)<L<f(b), найдется такая точка c, принадлежащая (а, в), в которой f(c)=L.

Теорема 5. Если у=f(x) непрерывная на промежутке J (замкнутое и нет, конечное или бесконечное), то множество У – ее значений на J также представляет собой промежуток, причем, если f(x) имеет обратную f^--1(x) на J, то эта последняя непрерывна на J.

Классификация точек разрыва функции.

Определение. Точка х₀ называется точкой устранимого разрыва функции у=f(x), если 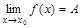, но f(x₀) ≠А или f(x) не определена в точке х₀. Пример: Функция sinx/ x при х=0 не определена, предел =1.

Определение. Точка х₀ называется точкой разрыва 1 рода функции у=f(x), если односторонние пределы f(x) при х→х₀ существуют, конечны и не равные друг другу. Пример. f(x)=Sign(x).

Определение. Точка х₀ называется точкой разрыва 2 рода функции у=f(x), если в этой точке функция не имеет хотя бы одного из односторонних пределов, или по крайней мере один из них бесконечен. Пример. У=1/х., у=е^1/х.