Методы решения тригонометрических уравнений. 1. Решение уравнений разложением на множители:

1. Решение уравнений разложением на множители:

а)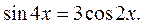

Воспользуемся формулой синуса двойного угла. Уравнение запишется в виде 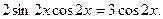Разложим левую часть уравнения на множители 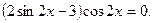Далее решаем совокупность уравнений, получаем

Ответ: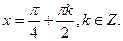

б) .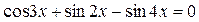

Воспользуемся формулой преобразования разности синусов в произведение, перепишем исходное уравнение в виде:

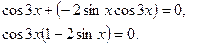Уравнение равносильно совокупности уравнений:

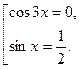
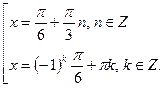Первое множество целиком содержит в себе второе множество, поэтому в ответ записывается только оно.

Ответ: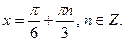

в) 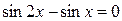Ответ: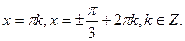

г) 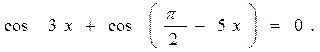Применяя формулу суммы косинусов, получим 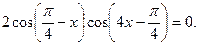Решая совокупность уравнений, получаем ответ.

Ответ: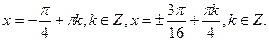

д) 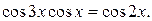Запишем уравнение в виде 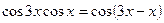. Применим формулу косинуса разности, получим

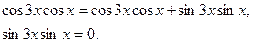Для нахождения корней, решим совокупность двух уравнений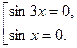

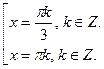
Числа вида 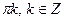находятся среди чисел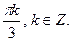

Ответ: .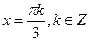

е) 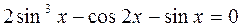Сгруппируем первый член с третьим, используем формулу двойного угла .

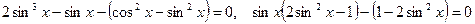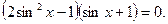
Ответ: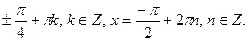

Примечание:

В вышеназванной статье из журнала «Математика в школе» приводится набор разноуровневых диагностических материалов по теме «Решение тригонометрических уравнений», а также дидактических материалов по разделам: решение простейших тригонометрических уравнений; уравнения, решаемые сведением к квадратному; методом разложения на множители; решение однородных уравнений.

2. Тригонометрические уравнения, приводимые к квадратным и уравнениям высших степеней.

Если тригонометрическое уравнение целого вида содержит только синусы или (и) косинусы, то область допустимых значений переменной – множество действительных чисел, т.к. эти функции определены для любого действительного значения. С помощью равносильных преобразований нужно привести уравнение к такому виду, чтобы какую-то функцию или их комбинацию принять за новую переменную. Решаем данные уравнения методом введения замены переменного. Например:

а)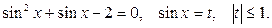

Ответ: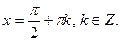

б) 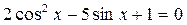. Ответ: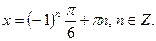

в) 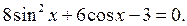Ответ: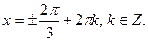

г)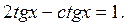

ОДЗ: 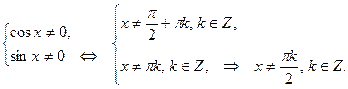Введем замену переменного 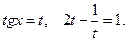Решаем уравнение, получаем

Ответ: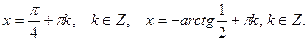

д) 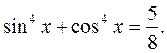Дополним уравнение до полного квадрата: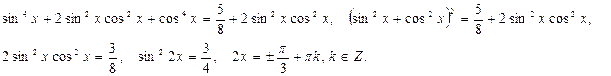

Ответ: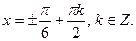

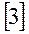
е) 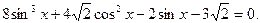Воспользовавшись основным тригонометрическим тождеством, перепишем в виде 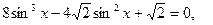введем переменную 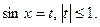Запишем уравнение относительно новой переменной: 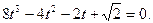Уравнение кубическое, угадаем один корень: 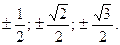При подборе корня разумно воспользоваться числами, представляющими собой табличные значения значения функции синус. Подстановка первого же из значений 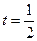, обращает левую часть в верное равенство. Разделим многочлен 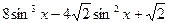на 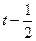, получим 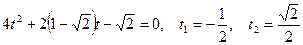- корни уравнения.

Ответ: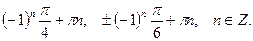

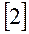
3. Однородные тригонометрические уравнения.

Уравнения вида 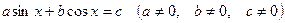называются однородными уравнениями первой степени относительно sinx и cosx. Уравнения при с=0 принимают вид 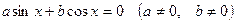, и решаются делением обеих частей на 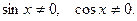В результате получается уравнение вида 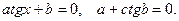(Здесь необходимо сослаться на Комментарии из Г.В. Дорофеев, Г.К. Муравин, Е.А. Седова. «Подготовка к письменному экзамену за курс средней школы» стр. 193, по поводу деления на cosx, и больше к этому не возвращаться)

Уравнение вида 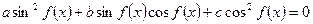называют однородным уравнением второй степени относительно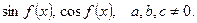 . Для решения этого уравнения нужно поделить обе части уравнения на 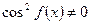и получаем уравнение .

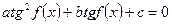Решим уравнение:

a) 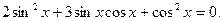делим обе части на 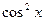и получаем 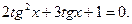Введем замену. Найдем корни квадратного уравнения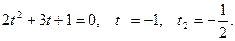

Ответ: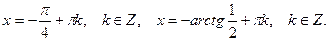

b) 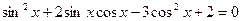. Воспользуемся основным тригонометрическим тождеством, уравнение примет вид 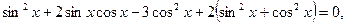получим 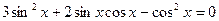. Решая по алгоритму, получаем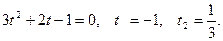

Ответ: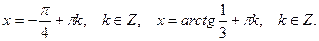

c)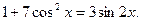

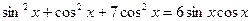, преобразуем, действуя по алгоритму, получаем:

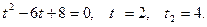
Ответ: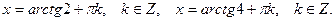

Остановимся на решении линейных однородных уравнений общего вида 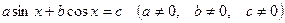. Существует три способа решения данных уравнений.

1 способ: Переход к аргументу 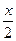. Пусть

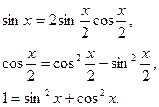
рассмотрим на примере

d) 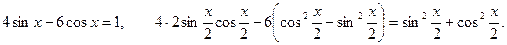После преобразований получаем 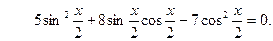Это однородное уравнение. Решаем по алгоритму. Получаем: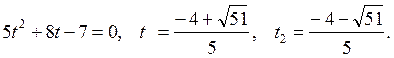

Ответ: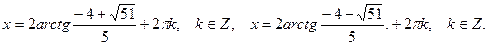

2 способ: Универсальная тригонометрическая подстановка. Выразим входящие в данное уравнение тригонометрические функции через тангенс половинного угла.

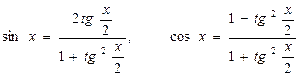
При таком переходе возможна потеря решений; следует помнить, что исходное уравнение имело смысл при всех значениях переменной х, тогда как выражение 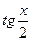не определено при 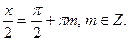Именно эти значения могут быть потеряны. Поэтому такие значения необходимо проверять отдельно, подставляя в исходное уравнение.

e) Решим уравнение: 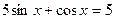. Получим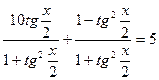

Преобразуем, приводим подобные, получаем: 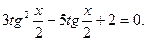Введем новую переменную 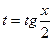. Решим уравнение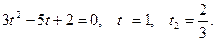

Ответ: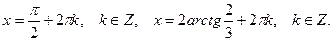

3 способ: введение вспомогательного угла. Пусть 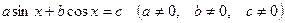. Разделим обе части этого уравнения н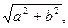а тогда

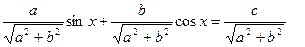. Введем вспомогательный аргумент j такой, что 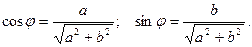Такое число j существует, т.к. 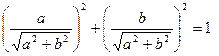Таким образом, уравнение можно записать в виде: .

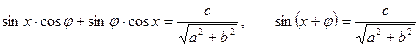f) Решим уравнение 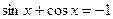. Поделим обе части на .

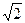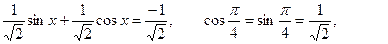Уравнение можно записать в виде: 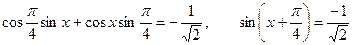. Решаем уравнение, получаем

Ответ: ,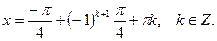

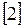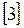
Date: 2015-09-24; view: 1609; Нарушение авторских прав