Методы решения тригонометрических уравнений

Решение тригонометрических уравнений.

Борисова Елена Анатольевна,

учитель математики

гимназии № 104 «Интеллектуал »,

Слушатель образовательной программы

Математическое образование

в основной и профильной школе»

Екатеринбург

Г.

Содержание:

Решение простейших тригонометрических уравнений.

Методы решения тригонометрических уравнений.

1. Решение уравнений разложением на множители:

2. Тригонометрические уравнения, приводимые к квадратным и уравнениям высших степеней.

3. Однородные тригонометрические уравнения.

• Переход к половинному аргументу
• Универсальная тригонометрическая замена
• Введение вспомогательного аргумента.

4. Уравнения вида , где Р(х,у) – многочлен.

5. Решения уравнений, содержащих тригонометрические функции под знаком радикала.

6. Использование ОДЗ при решении тригонометрических уравнений.

Заключение, или слово к руководителям семинара.

Литература.

1.

2. 3.

4.

5. С .Н. Олехник, М.К. Потапов, П.И. Пасиченко Нестандартные методы решения уравнений и неравенств. Московский Университет. 1991 г.

6. П .Горнштейн, А. Мерзляк. В Полонский, М. Якир. Экзамен по математике и его подводные рифы «Илекса М.2004 г.»

7..В. Дорофеев, Г.К. Муравин, Е.А. Седова. «Подготовка к письменному экзамену за курс средней школы»

.
Решение простейших тригонометрических уравнений.

Основная задача при решении стандартных тригонометрических уравнений состоит в приведении данного уравнения к квадратному или линейному уравнению относительно одной и той же тригонометрической функции одного и того же аргумента, то есть фактически к приведению исходного уравнения к простейшему тригонометрическому уравнению вида или к совокупности подобных уравнений. Для успешного решения задач по тригонометрии необходимо уверенное владение основными тригонометрическими формулами.

Кроме основных формул для решения уравнений удобно было использовать следующие формулы для корней уравнения:

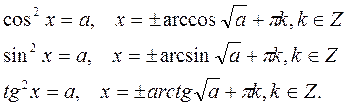
Решить уравнение: (cos2x - ½)(cos3x + ½)cos2x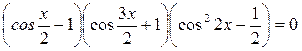

Решение: Область определения – х - любое действительное число. Левая часть уравнения содержит шесть сомножителей. Правая часть уравнения равна нулю. Произведение равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю. Следовательно, надо решить шесть уравнений.

1) cos2x - ½ = 0, cos2x = ½. 2x=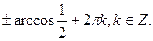

2х = 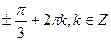, 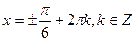. Следовательно, 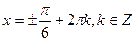являются корнями уравнения 1) и исходного уравнения.

2) cos3x + ½ = 0.

Следовательно, являются корнями уравнения 2) и исходного уравнения.

3) cos2x=0. 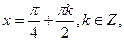являются корнями уравнения 3) и исходного уравнения.

4) 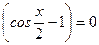, являются корнями уравнения 4) и исходного уравнения.

5) , являются корнями уравнения 5) и исходного уравнения.

6) 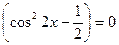, являются корнями уравнения 6) и исходного уравнения.

Ответ: ; ; ; ;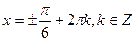

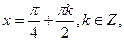
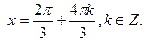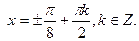
Решите уравнение:

.

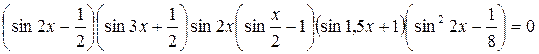Область определения - х – любое действительное число. Левая часть уравнения содержит шесть сомножителей, правая часть равна нулю. Произведение равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю. Следовательно, данное уравнение распадается на шесть уравнений.. Решим их.

1) .

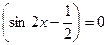2) . .

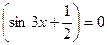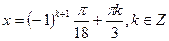3) .

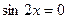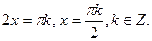
4) . 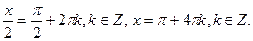Так как множество корней является подмножеством корней 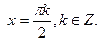(3), то эта серия корней не входит в окончательный ответ.

5) .

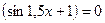6) .

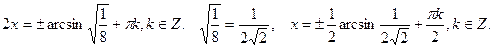
Ответ: ; ; ; ;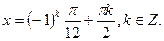

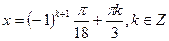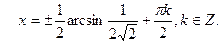
Решить уравнение: .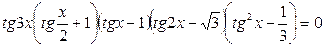

Решение: Найдем область определения данного уравнения:

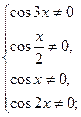
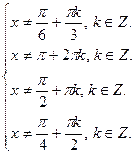
Нанесем все исключенные точки на одну единичную окружность:

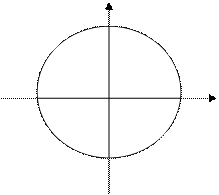Чтобы решить данное уравнение, надо приравнять каждый сомножитель нулю и решить получившиеся уравнения.

,

,

,

,

,

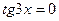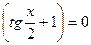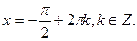
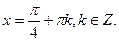
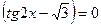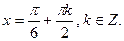
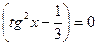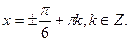
Нанесем получившиеся корни на единичную окружность. Из множества полученных корней отберем корни данного уравнения. Для этого нанесем все найденные решения на единичную окружность и исключим точки, не входящие в область определения.

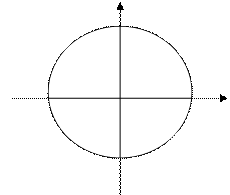
Ответ:

Date: 2015-09-24; view: 620; Нарушение авторских прав