
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Анализ работы системы ЧАПЧ
|
|
Основной задачей анализа работы системы ЧАПЧ является получение соотношений, описывающих поведение во времени частоты на выходе усилителя промежуточной частоты (рис. 6.1).Теоретический анализ процессов в системе ЧАПЧ проведем для фильтра низкой частоты (рис. 6.1) первого порядка при линеаризованных характеристиках частотного детектора в полосе 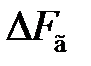 (рис. 6.2) и регулировочной характеристики генератора, управляемого напряжения, в полосе
(рис. 6.2) и регулировочной характеристики генератора, управляемого напряжения, в полосе 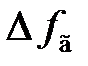 (рис. 6.3). При этом будем пренебрегать инерционностью УПЧ и использовать лишь статические характеристики (рис. 6.2, 6.3) частотного детектора и генератора, управляемого напряжением, без учёта переходных процессов в этих установках.
(рис. 6.3). При этом будем пренебрегать инерционностью УПЧ и использовать лишь статические характеристики (рис. 6.2, 6.3) частотного детектора и генератора, управляемого напряжением, без учёта переходных процессов в этих установках.
Основное уравнение для частот в тракте, приведенном на рис. 6.1, имеет вид

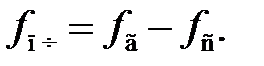 (6.1)
(6.1)
Тогда, полагая, что все частотные нестабильности отражены в отклонениях частоты входного сигнала 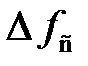 , запишем отклонение промежуточной частоты от своего среднего (номинального) значения в форме
, запишем отклонение промежуточной частоты от своего среднего (номинального) значения в форме
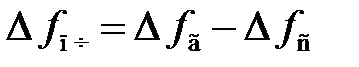 , (6.2)
, (6.2)
где 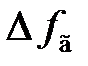 – отклонение частоты генератора управляемого напряжением от величины
– отклонение частоты генератора управляемого напряжением от величины 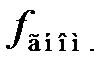 .
.
Для структурной схемы система ЧАПЧ (рис. 6.1) имеем [3]:
 (6.3)
(6.3)
Напряжение на выходе частотного детектора U чд связано с напряжением на выходе фильтра низких частот U Ф дифференциальным уравнением
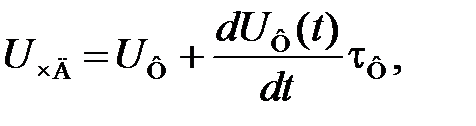 (6.4)
(6.4)
где для ФНЧ первого порядка (RC- фильтра) 
Рассмотрим процессы подстройки частоты при малых расстройках 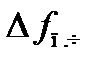 . Тогда зависимости
. Тогда зависимости 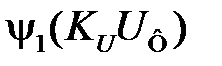 и
и 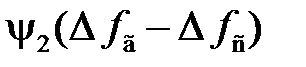 можно представить в следующем виде:
можно представить в следующем виде:
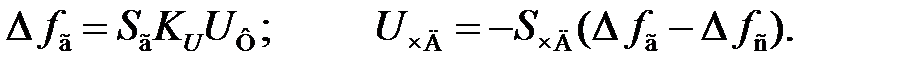 (6.5)
(6.5)
Здесь S г– крутизна регулировочной характеристики генератора, управляемого напряжением. Подставляя (6.4) в (6.5), получаем
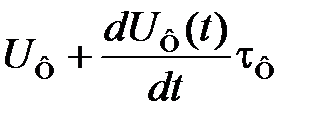
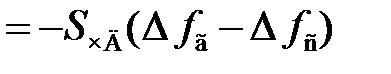 .
.
Учитывая, что из (6.5) 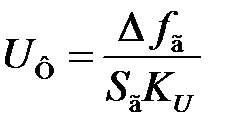 , имеем
, имеем


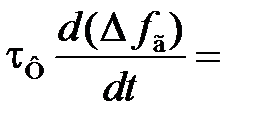
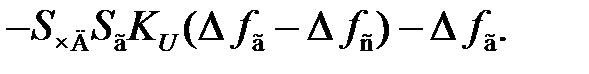 (6.6)
(6.6)
Запишем (6.5) в виде
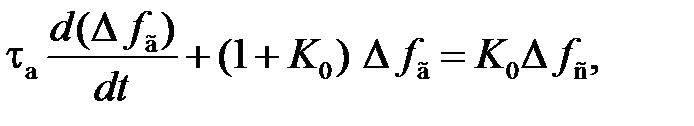 (6.7)
(6.7)
где  – коэффициент подстройки системы ЧАПЧ.
– коэффициент подстройки системы ЧАПЧ.
Решение линейного дифференциального уравнения (6.7) при нулевых начальных условиях может быть представлено в форме [3]


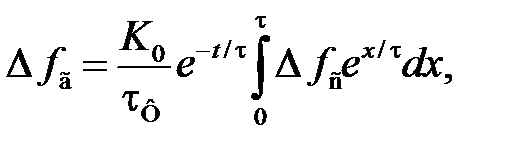 (6.8)
(6.8)
где 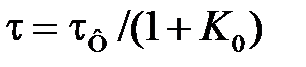 представляет собой постоянную времени системы ЧАПЧ.
представляет собой постоянную времени системы ЧАПЧ.
Если при t = 0 частота входного сигнала f с изменилась на некоторую величину 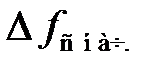 , не выходящую за пределы линейной аппроксимации статистической характеристики
, не выходящую за пределы линейной аппроксимации статистической характеристики 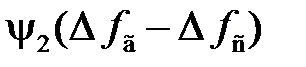 , то при
, то при 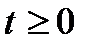 из (6.8) и (6.2) следует, что
из (6.8) и (6.2) следует, что
 (6.9)
(6.9)
Зависимость (6.9) приведена на рис. 6.4 для установившегося значения 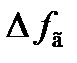 при t, стремящимся к бесконечности. Из (6.9) имеем
при t, стремящимся к бесконечности. Из (6.9) имеем
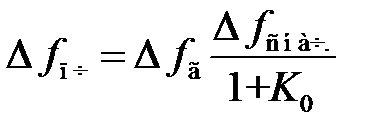 . (6.10)
. (6.10)
Как следует из (6.10), система ЧАПЧ уменьшает начальную расстройку частоты входного сигнала, вызванную действием дестабилизирующих факторов, причём количественная оценка этого уменьшения определяется величиной коэффициента подстройки ЧАПЧ. Эффективность системы ЧАПЧ определяется значениями S чд, S г и KU. В этой связи целесообразно использовать частотный детектор и генератор, управляемый напряжением, с возможно большими значениями крутизны характеристик.
Время установления t у частоты определим из (6.9) как время, прошедшее от начала процесса автоматической подстройки (t = 0) до момента достижения 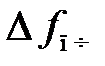 значения
значения 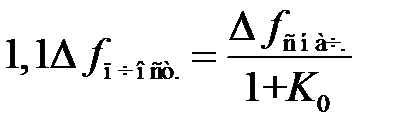 . Приравняв (6.9) этому значению, получим [2]
. Приравняв (6.9) этому значению, получим [2]
 (6.11)
(6.11)
Быстродействие системы ЧАПЧ при приеме частотно-модулированных сигналов ограничено требованием отсутствия демодуляции сигнала для самой низкой модулирующей частоты F м min. Вместе с тем система ЧАПЧ должна уменьшать расстройки, происходящие относительно медленно из-за влияния различных дестабилизирующих факторов, т.е. постоянная времени системы ЧАПЧ должна удовлетворять условиям
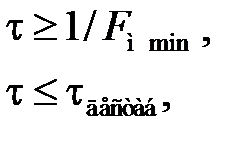 (6.12)
(6.12)
где 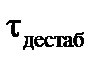 – «период» дестабилизирующих изменений частоты входного сигнала. Заметим, что система ЧАПЧ при любом значении постоянной времени τ неизбежно в той или иной степени снижает индекс частотной модуляции входного сигнала.
– «период» дестабилизирующих изменений частоты входного сигнала. Заметим, что система ЧАПЧ при любом значении постоянной времени τ неизбежно в той или иной степени снижает индекс частотной модуляции входного сигнала.
Уравнение (6.9) описывает работу системы ЧАПЧ в стационарном режиме при условии небольших начальных расстроек, когда справедливы линейные аппроксимации характеристик: детекторной (частотного детектора) и регулировочной (генератора управляемого напряжением). Как следует из рис. 6.5, регулировочная характеристика является прямой, проходящей под углом  к оси абсцисс.
к оси абсцисс.
Отметим, что при увеличении порядка фильтра низкой частоты порядок уравнения системы ЧАПЧ (6.7) повышается, и при числе звеньев более двух такая система ЧАПЧ может войти в режим самовозбуждения. Это может выражаться в появлении на выходе УПЧ дополнительной паразитной частотной и амплитудной модуляции.
При больших начальных расстройках начинают проявляться нелинейности элементов схемы системы ЧАПЧ. Проведем графический анализ работы системы ЧАПЧ при больших расстройках в стационарном режиме. Изобразим на детекторной характеристике частотного детектора (рис. 6.2) регулировочную характеристику ГУН. При этом учтём, что в стационарном режиме, в соответствии с (6.4), 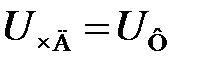 при
при 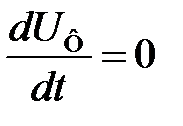 . Тогда, полагая
. Тогда, полагая 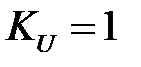 , имеем
, имеем 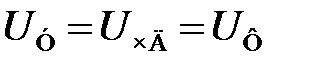 . Детекторная характеристика (рис. 6.2) переносится в область частот f г добавлением к каждому значению f пч величины
. Детекторная характеристика (рис. 6.2) переносится в область частот f г добавлением к каждому значению f пч величины 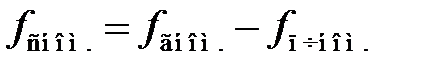 .
.
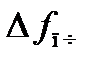
|

|
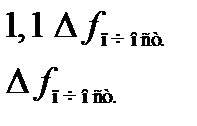
|
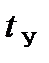
|
| t |
Рис. 6.4. Характеристика установления частоты в системе ЧАПЧ
с ФНЧ первого порядка
Совмещенные характеристики изображены на рис. 6.6. В пол. 1 регулировочной характеристики дестабилизирующие факторы отсутствуют и 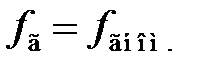 при
при  . Из-за влияния дестабилизирующих факторов на генератор, управляемый напряжением, регулировочная характеристика смещается вдоль оси частот. Кривая 2 показывает состояние системы ЧАПЧ при увеличении частоты ГУН на величину
. Из-за влияния дестабилизирующих факторов на генератор, управляемый напряжением, регулировочная характеристика смещается вдоль оси частот. Кривая 2 показывает состояние системы ЧАПЧ при увеличении частоты ГУН на величину  относительно
относительно 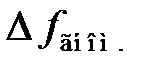 . При этом на выходе ЧД появляется положительное напряжение, которое снижает частоту ГУН (рис. 6.3).
. При этом на выходе ЧД появляется положительное напряжение, которое снижает частоту ГУН (рис. 6.3).
| 450 |
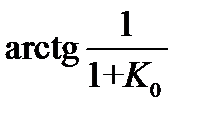
|
| при отсутствии системы ЧАПЧ |
| при наличии системы ЧАПЧ |
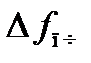
|
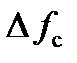
|
Рис. 6.5. Зависимость частоты на выходе УПЧ
от начальной расстройки
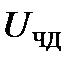
|
| f г |
| f г ном. |
| Г НОМГ |
| ff |
| +D |
| f г ном. + Δ f г |
| детекторная характеристика |
| регулировочная |
| характеристика |
| f |
Рис. 6.6. Детекторная и регулировочная характеристики
системы ЧАПЧ
Снижение частоты будет происходить до тех пор, пока не уравняются напряжение 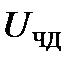 , создаваемое частотным детектором, и напряжение
, создаваемое частотным детектором, и напряжение 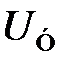 , необходимое для генерации данной частоты. Этому положению соответствует точка пересечения характеристик ЧД и ГУН. Таким образом, вместо начальной расстройки
, необходимое для генерации данной частоты. Этому положению соответствует точка пересечения характеристик ЧД и ГУН. Таким образом, вместо начальной расстройки  будет остаточная расстройка
будет остаточная расстройка  . Её величина определяется выражением (6.10).
. Её величина определяется выражением (6.10).
| Полоса удержания |
| Полоса втягивания |
| f г ном. |
| f |
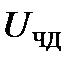
|
(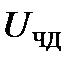 )max )max
|
Рис. 6.7. Детекторная и регулировочная характеристики системы ЧАПЧ

|
| при наличии системы ЧАПЧ |
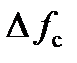
|
| полоса удержания |
| полоса втягивания |
| при отсутствии системы ЧАПЧ |
Рис. 6.8. Регулировочная характеристика системы ЧАПЧ
Если начальная расстройка выходит за пределы «полосы втягивания», но остается в пределах «полосы удержания», ограниченной точками пересечения с осью частот регулировочных характеристик, являющихся внешними касательными детекторной характеристики ЧД (рис. 6.7), то появляются три точки пересечения этих характеристик. Точка 1 является устойчивой и в ней выполняется условие подстраивающего действия системы ЧАПЧ. При работе точке 2 система ЧАПЧ не является устойчивой, т.к. при любых случайных отклонениях частоты 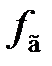 , генерируемая частота переходит в точки 1 и 3. В последнем случае система ЧАПЧ прекращает подстраивающее действие.
, генерируемая частота переходит в точки 1 и 3. В последнем случае система ЧАПЧ прекращает подстраивающее действие.
При начальной расстройке в пределах от 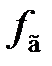 до границы «полосы удержания» система ЧАПЧ будет осуществлять подстраивающее действие. Наоборот, если происходило уменьшение начальной расстройки за пределами «полосы удержания» до границы «полосы втягивания», то система ЧАПЧ не будет производить подстройку частоты, пока начальная расстройка не окажется в «полосе втягивания».
до границы «полосы удержания» система ЧАПЧ будет осуществлять подстраивающее действие. Наоборот, если происходило уменьшение начальной расстройки за пределами «полосы удержания» до границы «полосы втягивания», то система ЧАПЧ не будет производить подстройку частоты, пока начальная расстройка не окажется в «полосе втягивания».
Описанные процессы соответствуют регулировочной характеристике системы ЧАПЧ, представленной на рис. 6.8. Характерным является наличие «гистерезисной петли» [2],обусловленной различием величин «полосы втягивания» и «полосы удержания».
На рис. 6.8 условно показаны возможные сложные траектории (пунктирные линии) перехода системы ЧАПЧ из рабочей области в область отсутствия подстройки по частоте. Ширина «полосы удержания», и «полосы втягивания» пропорциональна полосе пропускания  частотного детектора и тем больше, чем больше K 0.
частотного детектора и тем больше, чем больше K 0.
Date: 2015-09-24; view: 1121; Нарушение авторских прав