Оценка разброса

Как мы уже отмечали, характер распределения результатов после воздействия изучаемого фактора в опытной группе дает существенную информацию о том, как испытуемые выполняли задание. Сказанное относится и к обоим распределениям в контрольной группе:

Контрольная группа Мода (Мо) Медиана (Me) Средняя М\)

Ф°":....................................

После воздействия:....................................

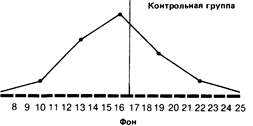
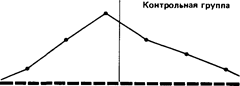
8 9 10 11 12 1314 1516 171819 2021 22232425 После воздействия

Сразу бросается в глаза, что если средняя в обоих случаях почти одинакова, то во втором распределении результаты больше разбросаны, чем в первом. В таких случаях говорят, что у второго распределения больше диапазон, или размах вариаций, т. е. разница между максималь­ным и минимальным значениями.

Так, если взять контрольную группу, то диапазон распределения для фона составит 22 — 10 = 12, а после воздействия 25 — 8 = 17. Это позво­ляет предположить, что повторное выполнение задачи на глазодвига-тельную координацию оказало на испытуемых из контрольной группы определенное влияние: у одних показатели улучшились, у других ухуд­шились¹. Однако для количественной оценки разброса результатов

' Здесь мог проявиться зффект п.шцебо, связанный с тем. что запах дыма травы вызвал у испытуемых уверенность в том, что они находятся под воз­действием наркотика. Для проверки этого предположения следовало бы повто­рить эксперимент со второй контрольной группой, в которой испытуемым будуг 1;|вать только обычную сигарету.

относительно средней в том или ином распределении существуют более точные методы, чем измерение диапазона.

Чаще всего для оценки разброса определяют отклонение каждого из полученных значений от средней (М-М), обозначаемое буквой d, а затем вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Напротив, если эта средняя невелика, то данные больше сконцентриро­ваны относительно их среднего значения и выборка более однородна.

Итак, первый показатель, используемый для оценки разброса,-это среднее отклонение. Его вычисляют следующим образом (пример, кото­рый мы здесь приведем, не имеет ничего общего с нашим гипотетиче­ским экспериментом). Собрав все данные и расположив их в ряд

356911 14, находят среднюю арифметическую для выборки:

3+5+6+9+11+14 48

__————^———————=^=8.

Затем вычисляют отклонения каждого значения от средней и сумми­руют их:

-5 -3 -2 +1 +3 +6 (3 - 8) + (5 - 8) + (6 - 8) + (9 - 8) + (11 - 8) + (14 - 8).

Однако при таком сложении отрицательные и положительные отклоне­ния будут уничтожать друг друга, иногда даже полностью, так что результат (как в данном примере) может оказаться равным нулю. Из этого ясно, что нужно находить сумму абсолютных значений индиви­дуальных отклонений и уже эту сумму делить на их общее число. При этом получится следующий результат:

Общая формула:

2^| п

Среднее отклонение =

где Т. (сигма) означает сумму; | d\ - абсолютное значение каждого инди­видуального отклонения от средней; и-число данных.

Однако абсолютными значениями довольно трудно оперировать в алгебраических формулах, используемых в более сложном статистиче­ском анализе. Поэтому статистики решили пойти по «обходному пути», позволяющему отказаться от значений с отрицательным знаком, а имен­но возводить все значения в квадрат, а затем делить сумму квадратов на

Приложение Б

число данных. В нашем примере это выглядит следующим образом:

(_5)² + (-З)² + (-2)² + (+1)² + (+3)² + (+6)² _

6 _25+9+4+1+9+36_84_

6 ^- 6 ~ '

В результате такого расчета получают так называемую вариансу¹ Формула для вычисления вариансы, таким образом, следующая:

Варианса -=•

Наконец, чтобы получить показатель, сопоставимый по величине со средним отклонением, статистики решили извлекать из вариансы квад­ратный корень. При этом получается так называемое стандартное отклонение:

Стандартное отклонение =

В нашем примере стандартное отклонение равно ^14 = 3,74.

Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не п, an—I:

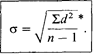
Вернемся теперь к нашему эксперименту и посмотрим, насколько полезен оказывается этот показатель для описания выборок.

На первом этапе, разумеется, необходимо вычислить стандартное

* Варианса представляет собой один из показателей разброса, используемых в гекоторых статистических методиках (например, при вычислении критерия F, <.м. следующий раздел). Следует отметить, что в отечественной литературе вариансу часто называют дисперсией. -Прим. перед.

* Стандартное отклонение для популяции обозначается маленькой греческой буквой сигм! (ст), а для выборки - буквой s. Это касается и вариансы, т.е кзадрага стандартного отклонения, для популяции она обозначается ет², а для выборки s².

Статистика и обработка данных

отклонение для всех четырех распределений. Сделаем это сначала для фона опытной группы:

Date: 2015-09-22; view: 543; Нарушение авторских прав