Задание № 2. Описать назначение и функциональные возможности указанных в варианте задания программ для компьютера

Описать назначение и функциональные возможности указанных в варианте задания программ для компьютера, системных операций или операций, выполняемых пользователем в офисных приложениях. Отметить особенности последних версий используемых программных средств.

Табличные процессоры: возможности MS Excel при решении задач линейного программирования. Линейная оптимизация.

Линейное программирование часть математического программирования, посвященная теории и методам решения экстремальных задач, нахождения минимума или максимума функции цели, характеризующихся линейной зависимостью между неизвестными переменными.

Применение методов линейного программирования актуально в настоящее время, так как использование математических моделей является важным направлением совершенствования планирования и анализа деятельности фирм. Формулировка задачи в виде математической модели позволяет конкретизировать информацию, сделать задачу более наглядной, создавать и моделировать варианты, выбирать оптимальные, наиболее рациональные решения из возможных альтернатив.

Математическое программирование – раздел математики, разрабатывающий теоретическое обоснование и способы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции нескольких переменных с ограничениями на область допустимых значений неизвестных переменных.

Имеющиеся ресурсы представляются в виде системы ограничений. Функцию, экстремальное значение которой нужно найти называют целевой, показателем эффективности или критерием оптимальности. Именно эти две составляющие являются необходимыми компонентами математической модели задачи.

В большинстве случаев модель в некотором роде заменяет сам исследуемый объект, то есть оригинал. При решении задач вместо исходного объекта (оригинала, словесного описания) используется его модель, в частности математическая. Модель являлась представлением объекта в некоторой форме, отличной от формы его реального существования.

Математическая модель задачи – это отображение исследуемого объекта в виде систем неравенств и уравнений, функций и т. д.

Линейное программирование – метод математического программирования, отыскания экстремума функции, с определенными ограничениями, выраженных в виде системы линейных неравенств или уравнений. Здесь линейность заключается в том, что если изображать все ограничения и целевую функцию на системе координат, то графически они будут представлены в виде прямых линий [10].

Суть решения задачи линейного программирования включает необходимость нахождения таких условий, которые будут приводить функцию цели к минимуму или максимуму, то есть к экстремуму.

Условия задачи представлены в виде системы линейных уравнений, показывающих ограничения имеющихся в наличии ресурсов:

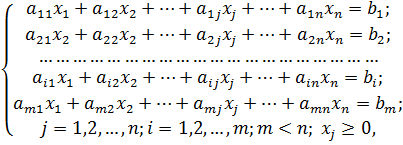(1.1)

где x_j– неизвестные переменные, содержащие решение поставленной задачи;

a_ij и b_j– известные постоянные величины, характеризующие условия задачи.

Целевая функция задается в виде:

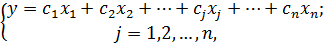(1.2)

где c_j– постоянные коэффициенты стоимости.

Ограничения могут быть, заданы не только в виде уравнений, но и в виде системы неравенств. В данном случае, для того чтобы привести систему неравенств к виду (1.1), нужно в каждое линейное ограничение ввести добавочные неотрицательные неизвестные: x_n+1, x_n+2, …,x_n+m.

Общая математическая формулировка задачи соответствует условиям (1.1) и (1.2).

Первая строка системы уравнений (1.1) соответствует выражению:

,

где a₁₁ – количество единиц ресурсов вида 1 на первом предприятии; a₁₂ – количество единиц ресурсов вида 1 на втором предприятии и т.п.;b₁ – общий объем ресурсов вида 1(для всех предприятий); x₁, x₂ и т.д. – искомое количество предприятий типов 1, 2 и т.д.

Вторая строка системы уравнений (1.1) содержит аналогичные величины для ресурсов вида 2 и т.д. Функция цели соответствует формуле (1.2). Требуется обратить в минимум величину

,

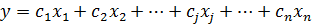где c_j– показатель, характеризующий издержки предприятий.

Пусть m – суммарное число разных типов ресурсов, которые есть у собственника, а n – число видов предприятий, между которыми эти ресурсы распределены. При этом известно, какое количество однородных ресурсов различного вида (i=1, 2, …,m) может быть реализовано на каждом из предприятий данного типа (j=1,2,…,n), а также общее количество ресурсов данного вида (b_i). Известно также относительное значение издержек на каждом из предприятий(c_j).

Задача заключается в том, чтобы наилучшим образом разделить имеющиеся ресурсы по предприятиям, то есть найти неизвестные величины x_j.

Таким образом, особенностями линейного программирования являются:

- линейная зависимость функции цели;

- область допустимых значений устанавливает система линейных уравнений или неравенств.

Табличными процессами называют пакеты программ, предназначенных для создания электронных таблиц и манипулирование их данными. Применение электронных таблиц упрощает работу с данными, позволяет автоматизировать вычисление без использования специального программирования. Наиболее широкое применение – в экономических и бухгалтерских расчетах. MS Excel предоставляет пользователю возможность:

1. Использовать сложные формулы, содержащие встроенные функции.

2. Организовывать связи ячеек и таблиц, при этом изменение данных в исходных таблицах автоматически изменяет результаты в итоговых таблицах.

3. Создавать сводные таблицы.

4. Применять к таблицам сортировку и фильтрацию данных.

5. Осуществлять консолидацию данных (объединение данных из нескольких таблиц в одну).

6. Использовать сценарии – поименованные массивы исходных данных, по которым формируются конечные итоговые значения в одной и той же таблице.

7. Выполнять автоматизированный поиск ошибок в формулах.

8. Защищать данные.

9. Использовать структурирование данных (скрывать и отображать части таблиц).

10. Применять автозаполнение.

11. Применять макросы.

12. Строить диаграммы.

13. Использовать автозамену и проверку орфографии.

14. Использовать стили, шаблоны, автоформатирование.

15. Обмениваться данными с другими приложениями.

Ключевые понятия:

1. Рабочая книга – основные документы, хранится в файле.

2. Лист (объем: 256 столбцов, 65536 строк).

3. Ячейка – наименьшая структурная единица размещения данных.

4. Адрес ячейки – определяет положение ячейки в таблице.

5. Формула – математическая запись вычислений.

6. Ссылка – запись адреса ячейки в составе формулы.

7. Функция – математическая запись, указывающая на выполнение определенных вычислительных операций. Состоит из имени и аргументов.

Ввод данных:

Данные могут быть следующих типов –

· Числа.

· Текст.

· Функции.

· Формулы.

Вводить можно –

· В ячейки.

· В строку формул.

Если на экране в ячейке после ввода появляется ########, значит число длинное и в ячейке не помещается, то надо увеличить ширину ячейки.

Формулы – определяют, каким образом величины в ячейках связаны друг с другом. Т.е. данные в ячейке получаются не заполнением, а автоматически вычисляются. При изменении содержимого ячеек, на которые есть ссылка в формуле, меняется и результат в вычисляемой ячейке. Все формулы начинаются знаком =. Далее могут следовать –

· Ссылка на ячейку (например, А6).

· Функция.

· Арифметический оператор (+, -, /, *).

· Операторы сравнения (>, <, <=, =>, =).

Можно вводить формулы прямо в ячейку, но удобнее вводить с помощью строки формул.

Функции – это стандартные формулы для выполнения определенных задач. Функции используются только в формулах.

Способ: Вставка – Функция или в строке формул щелкнуть на =. Появится диалоговое окно со списком десяти недавно использованных функций. Для расширения списка выбрать Другие функции…, откроется другое диалоговое окно, где функции сгруппированы по типам (категориям), приведено описание назначения функции и их параметров.

Полное описание по работе с электронными таблицами MS Excel, можно найти в учебниках и пособиях (специализированных).

Date: 2015-09-23; view: 585; Нарушение авторских прав