
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приклади розв’язування задач
|
|
Приклад 1. Дві паралельно з’єднаних елемента з ЕРС e1 = 2 В та e2 = 4 В та внутрішніми опорами r1 = 1 Ом та r2 = 1,5 Ом замкнуті на внутрішній опір R = 1,4 Ом. Знайти струм в кожному з елементів і в усьому колі.
Розв’язання. Довільно виберемо напрям струмів у контурах та напрям обходу. Для вузла А застосуємо перше правило Кірхгофа (рис. 6.)
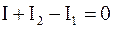 . (1)
. (1)
Для контурів Аe1BRA та Аe2BRA запишемо друге правило Кірхгофа:
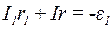 , (2)
, (2)
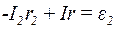 . (3)
. (3)
із (2)
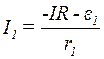 , (4)
, (4)
із (3)
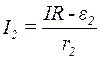 . (5)
. (5)
Підставивши (4) і (5) в (1), отримаємо
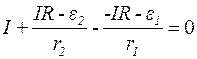 .
.
Підставляючи числові значення, знаходимо, що І = 0,2 А.
 Підставляючи числові значення в (4), знаходимо, що
Підставляючи числові значення в (4), знаходимо, що
І1 = -2,28 А.
Підставляючи числові значення в (5), знаходимо, що
І2 = -2,48 А.
Або, підставивши замість І та І1 їх значення в (1), отримаємо, що І2 = -2,48 А.
Від’ємні значення струмів І1 та І2 вказують на те, що ці струми течуть в зворотному напрямі.
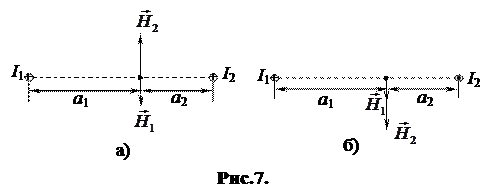
Приклад 2. По двох довгих паралельних прямолінійних провідниках, що знаходяться на відстані 5 см один від одного, течуть струми по І = 10 А у кожному. Визначити напруженість магнітного поля, створеного струмами в точці, яка лежить на відстані 3 см від першого провідника, для випадків:
а) струми течуть в одному напрямі;
б) струми течуть в протилежних напрямах.
Розв’язання. Результуюча напруженість магнітного поля дорівнює векторній (геометричній) сумі напруженостей полів, створених кожним струмом окремо (рис. 7.):
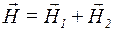 ,
,
де Н1 − напруженість поля, створеного струмом І1, Н2 − струмом І2.
Оскільки Н1 та Н2 напрямлені по одній прямій, то геометрична сума може бути замінена алгебраїчною сумою 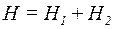 . При цьому Н1 та Н2 повинні бути взяті із відповідними знаками. Напрями векторів
. При цьому Н1 та Н2 повинні бути взяті із відповідними знаками. Напрями векторів 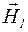 та
та 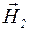 знайдемо за правилом свердлика.
знайдемо за правилом свердлика.
Для випадку а) 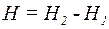 . Напруженість магнітного поля, створеного довгим прямим провідником зі струмом І, на відстані а від нього, визначається за формулою
. Напруженість магнітного поля, створеного довгим прямим провідником зі струмом І, на відстані а від нього, визначається за формулою 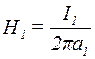 . Аналогічно
. Аналогічно 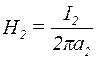 . Струми І1 = І2 = І. Тоді:
. Струми І1 = І2 = І. Тоді:
 |
а)
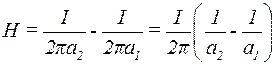 ,
,
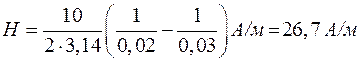 .
. 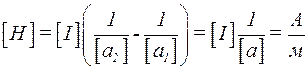
б)
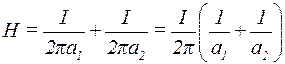 ,
,
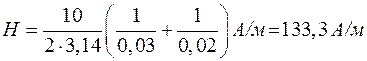 ;
;
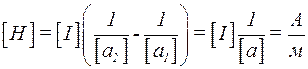
Приклад 3. Соленоїд довжиною 50 см і площею поперечного перерізу 10 см2 має 800 витків. Визначити магнітний потік через поперечний переріз соленоїда, якщо через соленоїд протікає струм 2 А.
Розв’язання. Магнітний потік, що пронизує поперечний переріз соленоїда, визначається формулою
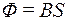 ,
,
де B − індукція магнітного поля, створеного струмом, що тече по витках соленоїда,
S − площа поперечного перерізу соленоїда.
Індукція магнітного поля B пов’язана з напруженістю Н поля співвідношенням
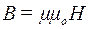 ,
,
де m − магнітна проникність в контурі,
mо − стала системи СІ, що дорівнює 12,57∙10-7 Гн/м.
Напруженість магнітного поля всередині соленоїда
 ,
,
де no − кількість витків на одиницю витків соленоїда
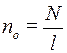 ,
,
де, в свою чергу, N − кількість витків на соленоїді, l − його довжина.
Тоді
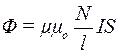 .
.
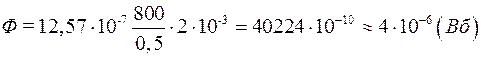
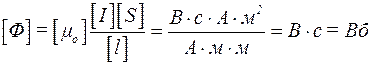
Приклад 4. Протон, прискорений різницею потенціалів U = 100 В, влітає в однорідне магнітне поле напруженістю 2,4∙103 А/м під кутом 60о до напряму напруженості поля. Визначити радіус і крок гвинтової лінії, по якій буде рухатись протон (маса протона − 1,67∙10-27кг, заряд − 1,6∙10-19 Кл).
Розв’язання. Кінетична енергія протона, що пройшов прискорюючу різницю потенціалів U, визначається рівністю:
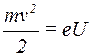 .
.
Звідси, швидкість протона
 ,
,
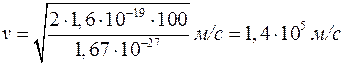 .
.
 |
На протон, що влетів до магнітного поля, діє сила Лоренца (рис.8.), перпендикулярна напруженості поля і нормальній складовій швидкості, тобто
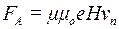 , (1)
, (1)
де m = 1, mо = 12,57∙10-7 Гн/м, e = 1,6∙10-19 Кл, Н − напруженість магнітного поля, vn − нормальна складова швидкості.
З рисунка видно, що
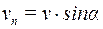 ,
,
де v − швидкість частинки,
a − кут між швидкістю та напруженістю поля.
Оскільки сила Лоренца є доцентровою силою,
Fл = Fд, (2)
то під дією сили Лоренца протон в магнітному полі буде рухатись по колу в площині, перпендикулярній до поля, зі швидкістю, що дорівнює нормальній складовій початкової швидкості.
Одночасно протон буде рухатись і вздовж поля зі швидкістю vr, що дорівнює складовій початкової швидкості у напрямку поля (vr = v∙cosa).
Радіус кола знайдемо із співвідношення (2):
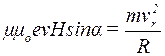 ,
,
де m − маса протона,
R − радіус кола.
Звідси
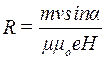 ,
,
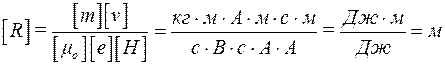
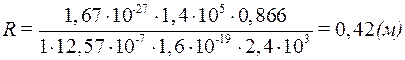 ,
,
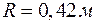 .
.
Крок h гвинтової лінії дорівнюватиме шляху, пройденому вздовж поля зі швидкістю vr за час, який потрібен протону для того, щоб здійснити оберт, і визначиться за формулою:
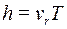 ,
,
де T − період обертання протона. Цей час знайдемо за формулою
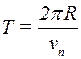 .
.
Підставивши цей вираз періоду в (3),матимемо
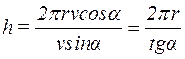 ,
,
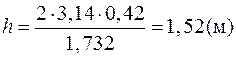 ,
,
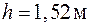 .
.
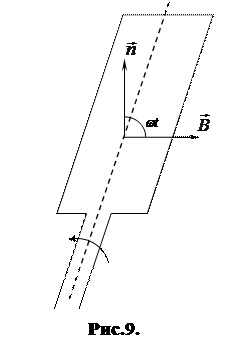
Приклад 5. В однорідному магнітному полі з індукцією B = 0,1 Тл рівномірно обертається рамка, що містить N = 1000 витків. Площа рамки S = 150 см2. Рамка робить n = 10 об/с. Визначити миттєве значення ЕРС, що відповідає куту повороту рамки на 30о.
Розв’язання. Миттєве значення ЕРС індукції визначається співвідношенням (рис.9.)
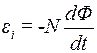 .
.
При обертанні рамки (див. рис. 9) магнітний потік Ф, що пронизує рамку в момент t, змінюється за законом:
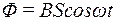 , (2)
, (2)
де B − магнітна індукція,
S − площа рамки,
w − циклічна частота, пов’язана з кількістю обертів за секунду співвідношенням
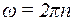 . (3)
. (3)
Підставивши (3) в (2) та про диференціювавши по часу, знайдемо миттєве значення ЕРС індукції:
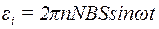
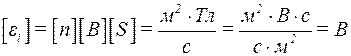
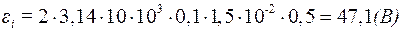
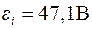 .
.
Приклад 6. На залізний стержень (m = 10 3) довжиною 50 см і перерізом 2 см2 намотаний в один шар провідник так, що на кожен сантиметр довжини стержня припадає 20 витків. Визначити енергію магнітного поля в сердечнику соленоїда, якщо сила струму в обмотці 0,5 А.
Розв’язання. Енергія магнітного поля соленоїда з індуктивністю L, по обмотці якого тече струм I, виражається формулою
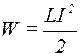 . (1)
. (1)
Індуктивність соленоїда залежить від кількості витків n, які припадають на одиницю довжини, від об’єму сердечника V та магнітної проникності m сердечника, тобто
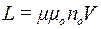 . (2)
. (2)
Підставивши (2) в (1), отримаємо:
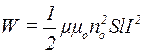 ,
,
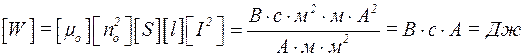
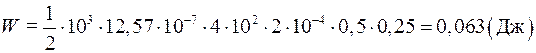 ,
,
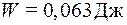 .
.
ОСНОВНІ ПОСТІЙНІ
Діелектрична проникність e
| Речовина | Значення |
| Вода | |
| Мастило | 2,2 |
| Парафін | 2,0 |
| Слюда | 7,0 |
| Скло | 7,0 |
| Фарфор | 5,0 |
| Ебоніт | 3,0 |
Date: 2015-09-22; view: 819; Нарушение авторских прав