
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Этап 5. Определение видимого угла падения и видимой мощности слоя, замеренных в косом разрезе
|
|
В геологии косым называется такой разрез, вертикальная секущая плоскость которого не перпендикулярна к наклонной структурной плоскости (кровле или подошве слоя). Если в нормальном разрезе секущая плоскость пересекает структурную плоскость S по линии падения uS, то в косом разрезе линией пересечения структурной плоскости S с плоскостью разреза является произвольная прямая m, определяющая направление и величину угла видимого падения слоя (рис. 5). Следует иметь в виду, что секущая плоскость D косого разреза пересечет не только кровлю слоя (плоскость S), но и его подошву (плоскость L). Таким образом, как и в нормальном разрезе, в косом мы получим две параллельные друг другу конкурирующие прямые т и п. Однако расстояние между прямыми т и n не соответствует истинному расстоянию между структурными плоскостями S и L, иначе говоря не определяет истинной мощности слоя: | mn | ¹ |SL|.
Решение задачи данного этапа следует начинать с проведения на плане проекции вертикальной секущей плоскости, которая по условию задачи составляет с направлением падения слоя угол, равный 50° (см. рис. 3). Отмечаем на плане проекции точек D, N и L пересечения плоскости разреза с изогипсами кровли (плоскость S) и подошвы (плоскость L) слоя. Прямая n определяется только одной точкой L, так как m || n.
Построение профиля косого разреза Б – Б (рис. 5) выполняется в левом нижнем углу формата (см. рис. 1). Замерив на профиле кратчайшее расстояние
между прямыми m и n и угол наклона прямой m (равно, как и прямой n) к горизонту, определим видимую мощность и видимый угол падения слоя (в косом разрезе Б – Б).
Видимая мощность слоя всегда больше его истинной мощности: Hв >H, а видимый угол падения меньше истинного: aв < aS. Полученные результаты указываются в ответе.
 Для проверки графических построений замерим расстояние в вертикальном направлении между прямыми m и n, полученное в косом разрезе, и прямыми uS и uL, полученное в нормальном разрезе. Эти расстояния должны быть равны между собой. Их называют вертикальной мощностью слоя Hверт. Вертикальная мощность не зависит от направления секущей плоскости и постоянна для любого направления разреза (см. рис. 4 и 5). Видимая мощность изменяется в зависимости от направления разреза: она увеличивается от значения истинной мощности в разрезе вкрест простирания до значения вертикальной мощности в разрезе, выполненном по направлению простирания слоя H < Hв < Hверт.
Для проверки графических построений замерим расстояние в вертикальном направлении между прямыми m и n, полученное в косом разрезе, и прямыми uS и uL, полученное в нормальном разрезе. Эти расстояния должны быть равны между собой. Их называют вертикальной мощностью слоя Hверт. Вертикальная мощность не зависит от направления секущей плоскости и постоянна для любого направления разреза (см. рис. 4 и 5). Видимая мощность изменяется в зависимости от направления разреза: она увеличивается от значения истинной мощности в разрезе вкрест простирания до значения вертикальной мощности в разрезе, выполненном по направлению простирания слоя H < Hв < Hверт.
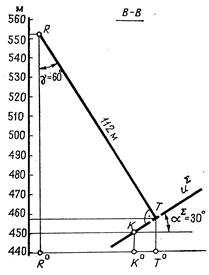
Этап 6. Определение зенитного угла и наклонной глубины скважины, запроектированной в точке R перпендикулярно к кровле слоя. Зенитным углом скважины называют линейный угол, составленный осью скважины и вертикальным направлением u, следовательно, величина зенитного угла дополняет угол наклона скважины к горизонту до 90°: gскв + aскв = 90°. Наклонной глубиной скважины с геометрической точки зрения будет истинная длина отрезка, соединяющего устье и забой скважины.
Определить указанные величины удобно по профилю разреза, выполненного вертикальной плоскостью, проходящей через точку R перпендикулярно к кровле слоя (плоскость S) (см. рис. 2). Плоскость разреза пересечет плоскость S по линии падения uS, кратчайшее расстояние от точки R(устья скважины) до которой на профиле разреза В – В и будет определять наклонную глубину скважины. Отметим на плане проекцию точки K пересечения плоскости разреза с одной из горизонталей плоскости S. Вторую точку, принадлежащую этой линии, строить не следует, так как угол падения плоскости S нам уже известен.
Линия вертикального масштаба при построении профиля разреза, выполненного по линии В – В, располагается в правой части формата (см. рис. 1). Отметки на этой линии наносят с учетом как отметки точки R, из которой проектируется скважина, так и отметки точки K. принадлежащей линии падения плоскости S (кровли слоя). При этом следует учесть место для надписи, которая сопровождает разрез, а также возможность определения точки пересечения линии падения uS с осью наклонной скважины, проведенной из точки R. Нанесем на профиле разреза проекции точек R (устья скважины) и K, принадлежащей uS (кровле слоя). Прямая uS пройдет через точку K и будет наклонена к линии горизонта под углом aS. По условию задачи скважина проектируется перпендикулярно к кровле слоя (плоскость S). Следовательно, на профиле разреза ее ось будет перпендикулярна к линии падения кровли (рис. 6). Точку пересечения оси скважины с кровлей слоя называют забоем скважины. Отрезок |RT| является наклонной глубиной скважины. Замерив длину |RT| и величину зенитного угла g, указываем полученные значения в ответе.
Оформление чертежа. Окончательное оформление чертежа выполняется согласно стандартам ЕСКД и ГОСТ 2.850 – 75 – ГОСТ 2.857 – 75 «Горная графическая документация». Проверив правильность решения задания, вместо точек A, B, C и R необходимо нанести условные знаки, обозначающие горные выработки, буровые скважины, обнажения и т. д. После чего чертеж обводится тушью.
Контрольная работа № 2. «Определение геометрических параметров геологической складки»
Задание.
Контрольная работа содержит 20 вариантов задания, для которых нижеприведенный текст является общим.
Вертикальные буровые скважины вскрыли в точках A, B, C и K, L, M крылья складки, поверхности которых могут быть представлены соответственно как плоскости S и L. Замок складки представляет собой цилиндрическую поверхность. Заданы координаты точек A, B, C и K, L, M и радиус цилиндрической поверхности R.Масштаб 1:5000.
Требуется определить: элементы залегания крыльев складки, величину угла складки mо, элементы залегания осевой (биссекторной) плоскости Q.
Исходные данные представлены в табл. 1.
Таблица 1
| Вариант 1 | Вариант 2 | |||||||||
| Плоскость | точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 50 мм | R = 70 мм | |||||||||
| Вариант 3 | Вариант 4 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 75 мм | R = 60 мм | |||||||||
| Вариант 5 | Вариант 6 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 80 мм | R = 55 мм | |||||||||
| Вариант 7 | Вариант 8 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 55 мм | R = 80 мм | |||||||||
| Вариант 9 | Вариант 10 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 65 мм | R = 75 мм | |||||||||
| Вариант 11 | Вариант 12 | |||||||||
| Плоскость | точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 75 мм | R = 105 мм | |||||||||
| Вариант 13 | Вариант 14 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 113 мм | R = 90 мм | |||||||||
| Вариант 15 | Вариант 16 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 120 мм | R = 83 мм | |||||||||
| Вариант 17 | Вариант 18 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 83 мм | R = 120 мм | |||||||||
| Вариант 19 | Вариант 20 | |||||||||
| Плоскость | Точка | Координаты, мм | Высотная отметка, м | Плоскость | Точка | Координаты, мм | Высотная отметка, м | |||
| x | y | x | y | |||||||
| S | A B C | S | A B C | |||||||
| L | K L M | L | K L M | |||||||
| R = 98 мм | R = 113 мм |
Геометрическая модель геологической складки
Первоначально рассмотрим геометрическую модель геологической складки: когда крылья складки представляют собой поверхности, близкие к плоскостям, складка может быть смоделирована двугранным углом SmL (рис. 1). Полуплоскости S и L моделируют крылья складки, криволинейная поверхность перехода одного крыла в другое Y носит название замка складки, а ребро двугранного угла m - шарнира складки. Биссекторная плоскость двугранного угла Q, проходящая через ребро m и биссектрису угла t, называется осевой плоскостью складки, а линия пересечения замка складки с осевой плоскостью – осью складки.
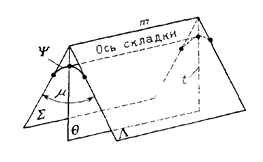
Рис. 1
Складки делятся на антиклинальные и синклинальные. У антиклинальных складок изгиб слоев происходит таким образом, что замок складки обращен вверх, а падение крыльев и осевой плоскости направлено от шарнира складки. У синклинальных складок замок обращен вниз, а падение крыльев и осевой плоскости направлено в сторону шарнира (рис. 2). Складки различают по положению осевой плоскости в пространстве и углам падения крыльев: складки с вертикальным расположением осевой плоскости - прямые или вертикальные; складки, у которых осевые плоскости наклонные, а крылья падают в разные стороны и под разными углами, - косые; складки, у которых крылья падают в одну сторону, - опрокинутые; складки с горизонтальным расположением осевой плоскости - лежачие; складки с осевой поверхностью, изогнутой до обратного падения - перевернутые. Обозначение шарнира в том и другом случаях показано на рис. 3.

Рис. 2
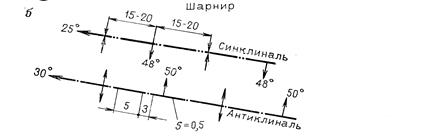
Рис. 3
Рекомендации по выполнению контрольного задания
Варианты с 1 по 10 контрольного задания выполняется на листе чертежной бумаги формата A3, варианты с 11 по 20 на формате А2 расположенном вертикально. В правом нижнем углу располагается основная надпись. В нижнем левом углу формата на расстоянии 5 мм от нижнего и левого края рамки выбирают точку начала отсчета координат. При этом ось х располагают вертикально, а ось у- горизонтально. По заданным (в табл. 1) координатам, в соответствии с вариантом, строятся проекции точек A, B, C, K, L, и M. Рядом с проекциями точек указывают их числовые отметки. На рис. 5 оставлены линии проекционной связи для точки M. Перейдя от задания крыльев складки (плоскостей S и L) точками к заданию горизонталями, строят их линию пересечения S´L = m и определяют элементы залегания. При построении единичного масштаба заложения необходимо обратить внимание на масштаб: в 1 см. – 50 м., а отметки горизонталей кратные 100.
Величина двугранного угла определяется линейным углом, составленным прямыми a и b пересечения его граней с плоскостью Т, перпендикулярной к ребру m. Биссекторная плоскость двугранного угла пройдет через ребро m и биссектрису b линейного угла m (рис. 4).
Алгоритм решения задачи.
1.Строят проекцию линейного угла m, которым измеряют двугранный угол SmL. Через точку E пересечения горизонталей hS 800 и hL 800 перпендикулярно к ребру m проводят вспомогательную плоскость T, соблюдая условия:

 hT ^ m, l T = 1/ l m, пад
hT ^ m, l T = 1/ l m, пад
Плоскость Т пересекает полуплоскости S и L (грани угла) по полупрямым a и b, которые и являются сторонами искомого угла m.
2. Истинную величину угла m определяют методом вращения плоскости Т вокруг ее горизонтали h900. Точки R и F, расположенные на оси вращения, не изменяют своего положения при вращении плоскости, точка E переместится по дуге окружности, проекция которой совпадает с проекцией ребра m. Истинную длину радиуса вращения точки E определяют построением профиля плоскости T. Новая проекция угла, составленного полупрямыми a и b, равна его истиной величине.
3. Через точку E900 проводят биссектрису t линейного угла до пересечения ее с осью вращения в точке N900. Если плоскость Т вращать в обратном направлении, то проекция биссектрисы займет положение t(N900E800). Биссектриса t и ребро m, как две пересекающиеся прямые, определяют в пространстве биссекторную плоскость Q(m´t) двугранного угла SmL.
4. Горизонталь h900 плоскости Q определяется точками N и D,имеющими одинаковые числовые отметки. Вторую горизонталь h800 проводят через точку E параллельно первой. Следует помнить, что Q является полуплоскостью, поэтому ее горизонтали – полупрямые.
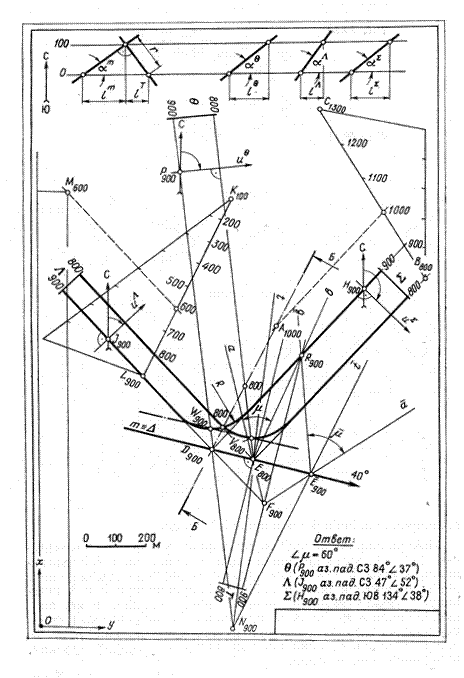
Рис. 4
Для построения замка складки, представляющего собой цилиндрическую поверхность, необходимо сопрячь горизонтали крыльев складки с одинаковыми числовыми отметками, заданными в условии радиусом R. Для этого, параллельно сопрягаемым горизонталям на расстоянии, равном радиусу, проводятся вспомогательные прямые линии. Точка их пересечения и будет центром сопряжения.
Шарнир складки пройдет через точки пересечения горизонталей осевой плоскости с горизонталями цилиндрической поверхности замка – W900 и V800.
Если на плане трудно отличить синклинальную складку от антиклинальной, то необходимо построить профиль разреза, пересекающего крылья, осевую плоскость и шарнир складки. Разрез проводят в свободном месте чертежа так, чтобы он не мешал другим построениям (на рис. 4 разрез по линии Б—Б). По профилю разреза, выполненного на рис. 5, можно сделать вывод о форме складки (профиль строится на черновике).
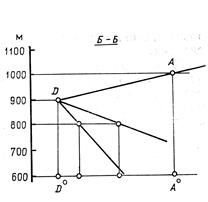
Рис. 5
После проверки задания окончательное оформление выполняется карандашом М, при этом вместо точек A, B, C, K, L и M наносятся условные обозначения вертикальных буровых скважин (на рис. 4 для лучшего понимания графических построений оставлены точки A, B, C, K, L и M).
СОДЕРЖАНИЕ
Проекции с числовыми отметками……………………………………….3
Точка………………………………………………………………………..3
Прямая линия……………………………………………………………3
Плоскость…………………………………………………………………….4
Взаимное расположение двух плоскостей……………………………5
Взаимное расположение прямой и плоскости…………………………..6
Метод вращения…………………………………………………………9
Пересечение поверхности с плоскостью………………………...……11
Пересечение поверхности с прямой линией………………..................12
Аксонометрические проекции………………………………………….14
Проекции точки и прямой…………………………………………………14
Проекции многогранников………………………………………………...14
Контрольные работы. Введение…………………………………………..15
Контрольная работа № 1. «Определение параметров
геологического пласта»………………………………………………………15
Контрольная работа № 2. «Определение геометрических
параметров геологической складки»……………………………………….27
Date: 2015-09-22; view: 1796; Нарушение авторских прав