Кореляційний зв'язок

Розглянемо вивід енергетичної характеристики як нелінійного кореляційного зв'язку.

На практиці приходиться зустрічатися з нелінійними кореляційними зв'язками, тобто такими зв'язками, коли приватні середні (дослідні точки) лягають певною подобою біля деякої кривої лінії, а не прямої.

При нелінійній регресії, насамперед, виникає питання визначення сили або тісноти зв'язку між Y і Х, що може бути різноманітною. К. Пірсон, як зазначено вище, запропонував у якості міри нелінійного зв'язку кореляційне відношення (11). До загальних властивостей кореляційного відношення можна додати наступне:

1. Якщо між Y і Х немає кореляційного зв'язку, то кореляційне відношення η дорівнює нулю і якщо зв'язок функціональний, то кореляційне відношення дорівнює одиниці.

2. Якщо ж, η=0 то Y не пов’язано з Х однозначним кореляційним зв'язок.

Ці дві властивості з’ясовують зміст крайніх значень кореляційного відношення. Сенс його проміжних значень пояснюється з тотожності:

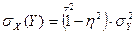(12)

Вона вказує, що при наближенні η до одиниці середня дисперсія Y по стовпчиках зменшується, наближаючись до нуля, а це показує, що зв'язок між Y і Х стає більш тіснішим. Це показує, що η дійсно є мірою кореляційного зв'язку будь-якого за формою. В цьому полягає велика перевага кореляційного відношення перед коефіцієнтом кореляції, що служить лише мірою лінійного кореляційного зв'язку.

В ряді випадків теоретичні і дослідні дані дозволяють припустити форму кривої, по якій можна зробити вимірювання, по методу найменших квадратів, приватних середніх щодо даної кривої.

Розглянемо загальний випадок параболічної залежності між Y і Х.

Звичайно парабола має вид:

Y=а₀+а₁∙х²+…+а_р∙х^р, (13)

і шукається за методом найменших квадратів. Коефіцієнти рівняння (13) визначаються таким чином, щоб сума:

оберталася в мінімум для знайдених значень.

Тоді повинні мати місце:

…

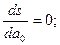
Ці рівняння легко приводяться до виду:

а₀∑п_х+а₁∑п_х∙х+…+ а_р∑п_х∙х^р=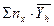

а₀∑п_х∙х+а₁∑п_х∙х²+…+ а_р∑п_х∙х^р+1=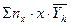

а₀∑п_х∙х^р+а₁∑п_х∙х^р+1+…+ а_р∑п_х∙х^2р=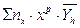

Тут:

п_х=п_h – число відліків при даному Х=х_h;

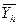- приватні середні (дослідні точки).

Вирішуючи цю систему знаходимо значення шуканих коефіцієнтів а₀, а₁, а₂…а_р, що звертають суму S в мінімум.

Поклавши в рівняння (13) Y=ω, а Х=1/А або одержимо загальний випадок гіперболічної залежності ω=f(А), тобто питомої витрати електроенергії від випуску продукції як нелінійного кореляційного зв’язку.

Date: 2015-09-22; view: 467; Нарушение авторских прав