
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Распределение Бернулли
|
|
Задание № 1
1. Построить распределение вероятности занятия линий в пучке из Vлиний в соответствии с распределениями Бернулли, Пуассона и Эрланга.
2. Для каждого распределения рассчитать математическое ожидание числа занятых линий, их дисперсию и среднеквадратическое отклонение.
Исходные данные для расчетов приведены в таблице 1.1 Величину Апринять равной А=а  V.
V.
Таблица 1.1
| № вар. | a | V |
| 2. | 0,25 |
Требования к выполнению задания:
1. Результаты расчета распределений представить в виде таблицы 1.2 и графика Pi = f(i).
| i | V | ||||||||
| Pi |
Таблица 1.2
На каждом графике привести значения математического ожидания, дисперсии, среднеквадратического отклонения и 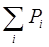 .
.
2. Расчеты проводить с точностью до четвертого знака после запятой.
В заключении провести анализ полученных результатов.
Решение:
Распределение Бернулли
Пусть исследуется пучок из Vлиний, каждая линия с вероятностью a может оказаться занятой и с вероятностью (1-a) – свободной. Тогда вероятность того, что в пучке из V линий окажется i любых линий занято, может быть определена из выражения
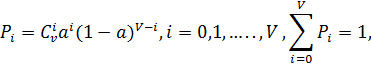
где 
Таблица 1.1
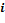
| 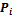
|
| 0.225 | |
| 0.3 | |
| 0.233 | |
| 0.116 | |
| 0.039 | |
| 0.0086 | |
| 0.0012 | |
| 0.0001 | |
Математическое ожидание и дисперсия числа занятых линий, вероятность занятия которых описывается распределением Бернулли, соответственно равны:


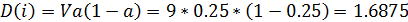
Средним квадратическим отклонением СВ называют корень квадратный из дисперсии:
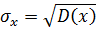
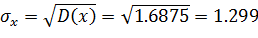
Date: 2015-09-25; view: 758; Нарушение авторских прав