Формулы Брейта-Вигнера

Ядерные реакции под действием нейтрона протекают в два этапа (Н. Бор 1936 г.): 1.Образование составного ядра О^* в квазистационарном состоянии с энергией возбуждения

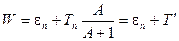, (1.68)

где ε_n - энергия связи нейтрона в ядре О^* , Т ‘ – кинетическая энергия нейтрона в системе центра инерции (ядро О^*).

Входной канал реакции .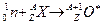

2.Распад промежуточного ядра после длительного времени жизни τ ~ 10^-14 сек происходит по каналу радиационного захвата нейтрона (n,γ) или по каналу неупругого рассеяния (n,n’). Другие каналы для простоты здесь мы рассматривать не будем. Вероятность распада составного ядра

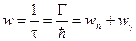(1.69)

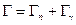- полная ширина уровня составного ядра, 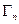- нейтронная ширина уровня

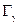- радиационная ширина уровня, 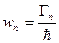- парциальная вероятность распада по нейтронному каналу, 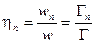- относительная вероятность распада по нейтронному каналу, 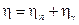- полная относительная вероятность распада составного ядра.

Спектр уровней энергии составного ядра остается дискретным, если энергия возбуждения ядра немного превышает энергию присоединения нейтрона W> 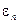≈ 8 Мэв. В этом случае расстояние между уровнями составного ядра Δ ~1 эв >>Г ≈ 0,1 эв больше ширины уровней этого ядра, т.е. уровни не перекрываются.

Если энергия налетающего нейтрона в системе центра инерции близка к энергии одного из уровней составного ядра, то вероятность образования составного ядра становится особенно большой. Сечение ядерной реакции резко возрастает, образуя резонансный максимум. Резонансные энергии соответствуют квазидискретным уровням составной системы.

Вероятность p нахождения составного ядра с энергией W около квазистационарного уровня W₀ определяется дисперсионным соотношением, (математической функцией «лоренцианом»)

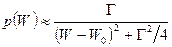. (1.70)

Поскольку кинетическая энергия нейтрона связана с энергией возбуждения составного ядра формулой (1.68), можно заменить (W-W₀)² = (T’-T₀’)².

Cечение реакции под действием нейтрона равно сечению σ^* образования составного ядра, умноженному на относительную вероятность η распада ядра по данному каналу.

Сечение радиационного захвата:

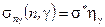(1.71)

Сечение неупругого рассеяния:

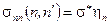. (1.72)

Сечение σ^* образования составного ядра равно геометрическому сечению S_l, умноженному на коэффициент прилипания ξ _l

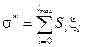(1.73)

Геометрическое сечение S_l равно доле всех частиц с орбитальным моментом l, летящих на ядро. Это площадь кольца со средним радиусом ρ_l с центром в ядре. Расстояние, на котором нейтрон пролетает около ядра 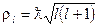, где 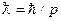-длина волны де Бройля. Тогда сечение

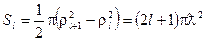. (1.74)

Если энергия налетающих нейтронов меньше 10 кэв, то длина волны велика по сравнению с размерами ядра(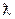 >> R), l_max = 0, S_l = S₀ = π 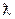².

Полагая коэффициент прилипания пропорциональным p (W), а также нейтронной ширине уровня, получаем ξ₀ ~ p(W) Г_n. Учет спинов, сталкивающегося нейтрона s, ядра мишени I и составного ядра J, приводит к появлению дополнительного множителя порядка единицы

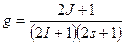(1.75)

в сечениях реакций, и, следовательно,

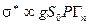. (1.76)

Подставляя (1.73-1.76) в (1.71)и (1.72) окончательно получаем формулы Брейта-Вигнера для сечения радиационного захвата нейтрона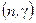

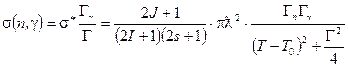, (1.77)

и для сечения неупругого резонансного рассеяния нейтрона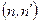

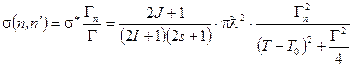(1.78)

Здесь g -спиновой множитель, T - кинетическая энергия нейтрона, T₀ - энергия нейтрона при которой наступает резонанс, т.е. кинетическая энергия нейтрона, соответствующая энергии W₀ изолированного уровня составного ядра О^*.

В формулах (1.77,1.78) первый сомножитель - спиновой, второй сомножитель - геометрическое сечение, третий сомножитель - резонансный.

Формула (1.78)справедлива также для сечения резонансного упругого рассеяния нейтронов σ(n,n) на ядре. Для медленных нейтронов процесс радиационного захвата нейтрона преобладает над упругим резонансным рассеянием.

Следствие1. Из формулы (1.77) следует, что вдали от резонанса T<<T₀ сечение радиационного захвата растет с уменьшением скорости нейтрона («закон 1/v»)

σ(n,γ)~1/ v. (1.79)

Действительно, пусть T<<T₀, g~ 1, тогда T-T₀<<1, 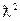~1/(mv)², Г=Г_n+Г_γ ≈ Г_γ, Г_n ~ 1/ 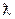~v и

σ(n,γ) ~ ~ .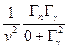

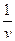Следствие 2. Без учета спинового множителя, при Т=Т₀ и Г ≈ Г_γ, максимальное сечение

σ₀(n,γ)= σ (Т₀)= 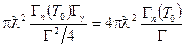. (1.80)

подставляя его в (1.77) получаем

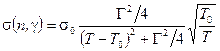. (1.81)

Е эв

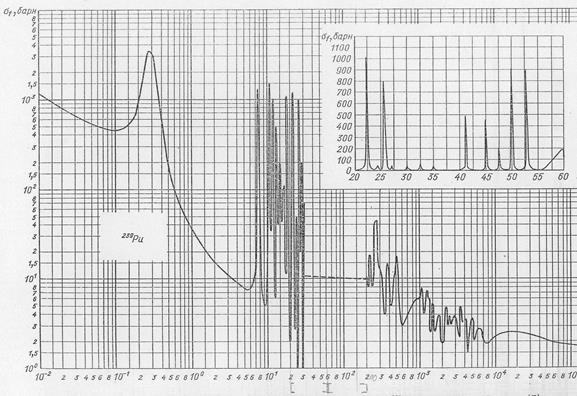
Рис.1.13. Сечение поглощения 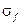для плутония-239 в зависимости от энергии нейтрона Е эв

В интервале низких энергий (10^-2 – 10^-1 эв) сечение пропорционально скорости («закон 1/v»). В двойном логарифмическом масштабе сечение поглощения в линейно меняется с изменением энергии нейтронов.

При значении 3 эв появляется первый сильный резонанс и последовательность меньших по величине резонансных пиков соответствующих дискретным уровням составного ядра.

Date: 2015-09-05; view: 1029; Нарушение авторских прав