
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Быстрый перевод числа из десятичной системы счисления в двоичную
|
|
Примеры:
· Переведем число 2 из десятичной системы. 2=21. Поэтому в двоичной системе число содержит 1 нуль. Впереди ставим "1" и получаем 102.
· Переведем 4 из десятичной системы. 4=22. Поэтому в двоичной системе число содержит 2 нуля. Впереди ставим "1" и получаем 1002.
· Переведем 8 из десятичной системы. 8=23. Поэтому в двоичной системе число содержит 3 нуля. Впереди ставим "1" и получаем 10002.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
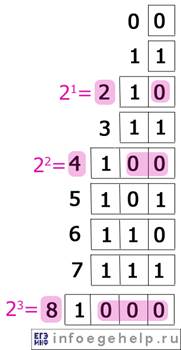
Аналогично и для других чисел "2 в степени".
Если число, которое нужно перевести, меньше числа "2 в степени" на 1, то в двоичной системе это число состоит только из единиц, количество которых равно степени.
· Переведем 3 из десятичной системы. 3=22-1. Поэтому в двоичной системе число содержит 2 единицы. Получаем 112.
· Переведем 7 из десятичной системы. 7=23-1. Поэтому в двоичной системе число содержит 3 единицы. Получаем 1112.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
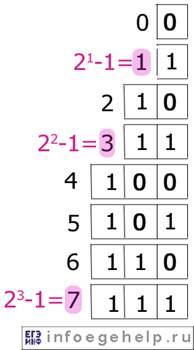
Аналогичен перевод и для других чисел "2 в степени-1".
Понятно, что перевод чисел от 0 до 8 можно сделать быстро или делением, или просто знать наизусть их представление в двоичной системе. Я привела эти примеры, чтобы Вы поняли принцип данного метода и использовали его для перевода более "внушительных чисел", например, для перевода чисел 127,128, 255, 256, 511, 512 и т.д.
Можно встретить такие задачи, когда нужно перевести число, не равное числу "2 в степени", но близкое к нему. Оно может быть больше или меньше числа "2 в степени". Разница между переводимым числом и числом "2 в степени" должна быть небольшая. Например, до 3. Представление чисел от 0 до 3 в двоичной системе надо просто знать без перевода.
Если число больше, то решаем так:
Переводим сначала число "2 в степени" в двоичную систему. А потом прибавляем к нему разницу между числом "2 в степени" и переводимым числом.
Например, переведем 19 из десятичной системы. Оно больше числа "2 в степени" на 3.
19=16+3.
16=24. 1610=100002.
310=112.
1910=100002+112=100112.
Если число меньше числа "2 в степени", то удобнее пользоваться числом "2 в степени-1". Решаем так:
Переводим сначала число "2 в степени-1" в двоичную систему. А потом вычитаем из него разницу между числом "2 в степени-1" и переводимым числом.
Например, переведем 29 из десятичной системы. Оно больше числа "2 в степени-1" на 2. 29=31-2.
3110=111112.
210=102.
2910=111112-102=111012
Если разница между переводимым числом и числом "2 в степени" больше трех, то можно разбить число на составляющие, перевести каждую часть в двоичную систему и сложить.
Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16.
512=29 . 51210=10000000002.
16=24. 1610=100002.
Теперь сложим столбиком:

1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
| n (степень) | |||||||||||
|
Пример. Число 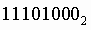 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
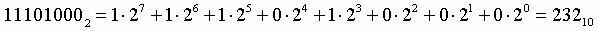
Билет 22
1. Оценка производительности идеального конвейера
Выполнение каждой команды складывается из ряда последовательных этапов (шагов, стадий), суть которых не меняется от команды к команде. С целью увеличения быстродействия процессора и максимального использования всех его возможностей в современных микропроцессорах используется конвейерный принцип обработки информации. Этот принцип подразумевает, что в каждый момент времени процессор работает над различными стадиями выполнения нескольких команд, причем на выполнение каждой стадии выделяются отдельные аппаратные ресурсы. По очередному тактовому импульсу каждая команда в конвейере продвигается на следующую стадию обработки, выполненная команда покидает конвейер, а новая поступает в него.
В различных процессорах количество и суть этапов различаются. Рассмотрим принципы конвейерной обработки информации на примере пятиступенчатого конвейера, в котором выполнение команды складывается из следующих этапов:
1. IF (Instruction Fetch) - считывание команды в процессор;
2. ID (Instruction Decoding) - декодирование команды;
3. OR (Operand Reading) - считывание операндов;
4. EX (Executing) - выполнение команды;
5. WB (Write Back) - запись результата.
Выполнение команд в таком конвейере представлено в табл. 11.1.
Так как в каждом такте могут выполняться различные стадии обработки команд, то длительность такта выбирается исходя из максимального времени выполнения всех стадий. Кроме того, следует учитывать, что для передачи команды с одной стадии на другую требуется определенное дополнительное время ( t), связанное с записью промежуточных результатов обработки в буферные регистры.
t), связанное с записью промежуточных результатов обработки в буферные регистры.
| Таблица 11.1. | |||||||||
| Команда | Такт | ||||||||
| i | IF | ID | OR | EX | WB | ||||
| i+1 | IF | ID | OR | EX | WB | ||||
| i+2 | IF | ID | OR | EX | WB | ||||
| i+3 | IF | ID | OR | EX | WB | ||||
| i+4 | IF | ID | OR | EX | WB |
Пусть для выполнения отдельных стадий обработки требуются следующие затраты времени (в некоторых условных единицах):
TIF = 20, TID = 15, TOR = 20, TEX = 25, TWB = 20.
Тогда, предполагая, что дополнительные расходы времени составляют dt = 5 единиц, получим время такта:
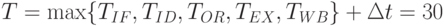 .
.
Оценим время выполнения одной команды и некоторой группы команд при последовательной и конвейерной обработке.
При последовательной обработке время выполнения N команд составит:
Tпосл = N*(TIF + TID + TOR + TEX + TWB) = 100N.
Анализ табл. 11.1 показывает, что при конвейерной обработке после того, как получен результат выполнения первой команды, результат очередной команды появляется в следующем такте работы процессора. Следовательно,
Tконв = 5T + (N-1) * T.
Примеры длительности выполнения некоторого количества команд при последовательной и конвейерной обработке приведены в табл. 11.2.
| Таблица 11.2. | |||||||||
| Количество команд | Время | ||||||||
| при последовательном выполнении | при конвейерном выполнении | ||||||||
Очевидно, что при достаточно длительной работе конвейера его быстродействие будет существенно превышать быстродействие, достигаемое при последовательной обработке команд. Это увеличение будет тем больше, чем меньше длительность такта конвейера и чем больше количество выполненных команд. Сокращение длительности такта достигается, в частности, разбиением выполнения команды на большое число этапов, каждый из которых включает в себя относительно простые операции и поэтому может выполняться за короткий промежуток времени. Так, если в микропроцессоре Pentium длина конвейера составляла 5 ступеней (при максимальной тактовой частоте 200 МГц), то в Pentium-4 - уже 20 ступеней (при максимальной тактовой частоте на сегодняшний день 3,4 ГГц).
Date: 2015-09-05; view: 1515; Нарушение авторских прав