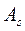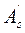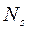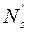Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Легкие сетки

Стр 1 из 10Следующая ⇒




Тип 4

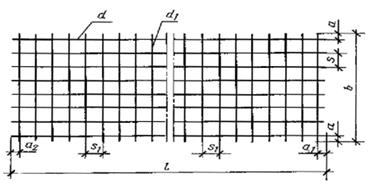
Тип 5


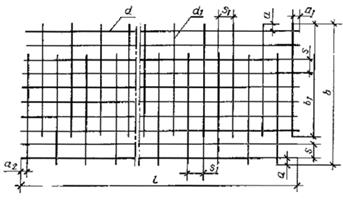
При соединении стержней арматуры классов A240, А300, A400, А500, A600, А800, A1000 разных диаметров должно соблюдать­ся условие d1 /d2 ≥ 0,85.

8. Наиболее распространенные изгибаемые элементы железобетонных конструкций—плиты и балки. Плитам и называют плоские элементы, толщина которых h\ значительно меньше длины 1\ и ширины Ь\. Балками называют линейные элементы, длина которых / значительно больше поперечных размеров h и Ь. Из плит и балок образуют многие железобетонные конструкции сборные и монолитные, а также сборно-монолитные. Армируют плиты сварными сетками. Сетки укладывают в плитах так, чтобы стержни их рабочей арматуры располагались вдоль пролета и воспринимали растягивающие усилия, возникающие в конструкции при изгибе под нагрузкой. Поэтому в пролетах плит сетки размещают понизу, а в многопролетных плитах — также и поверху над промежуточными опорами. Стержни рабочей арматуры принимают диаметром 3—10 мм, располагают их на расстоянии (с шагом) 100—200 мм один от другого. Защитный слой бетона для рабочей арматуры принимают не менее 10 мм, в особо толстых плитах (толще 100 мм) не менее 15 мм. Поперечные стержни принимают меньшего диаметра общим сечением не менее 10 °/о сечения рабочей арматуры, поставленной в месте наибольшего изгибающего момента; размещают их с шагом 250—300 мм, но не реже чем через 350 мм. Железобетонные балки могут быть прямоугольного, таврового, двутаврового, трапециевидного сечения. Высота балок h колеблется в широких пределах; она составляет l/l0—V20 часть пролета в зависимости от нагрузки и типа конструкции. В целях унификации высота балок назначается кратной 50 мм, если она не более 600 мм, и кратной 100 мм при больших размерах, из них предпочтительнее размеры, кратные 100 мм до высоты 800 мм, затем высоты 1000, 1200 мм н далее кратные 300. Ширину прямоугольных поперечных сечений Ь принимают в пределах (0,3—0,5) h, а именно 100, 120, 150, 200, 220, 250 мм и далее кратной 50 мм, из них предпочтительнее размеры 150, 200 мм и далее кратные 100.

9. Опыты с различными железобетонными элементами— изгибаемыми, внецентренно растянутыми, внецентренно сжатыми с двузначной эпюрой напряжений —показали, что при постепенном увеличении внешней нагрузки мож­но наблюдать три характерные стадии напряженно-де­формированного состояния: стадия I — до появления трещин в бетоне растянутой зоны, когда напряжения в бетоне меньше временного сопротивления растяжению и растягивающие усилия воспринимаются арматурой и бе­тоном совместно; стадия II — после появления трещин в бетоне растянутой зоны, когда растягивающие усилия в местах, где образовались трещины, воспринимаются арматурой и участком бетона над трещиной, а на участках между трещинами — арматурой и бетоном совместно; стадия III — стадия разрушения, характеризующаяся от­носительно коротким периодом работы элемента, когда напряжения в растянутой стержневой арматуре достига­ют физического или условного предела текучести, в высокопрочной арматурной проволоке—временного со­противления, а напряжения в бетоне сжатой зоны — вре­менного сопротивления сжатию; в зависимости от степени армирования элемента последовательность разру­шения зон растянутой и сжатой может изменяться.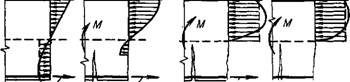

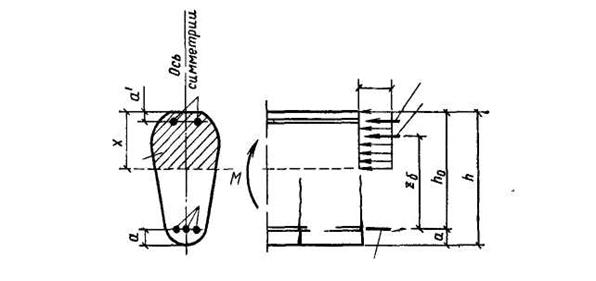
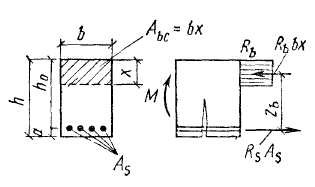
10. Расчет прочности по нормальным сечениям элементов любого симметричного профиля. Рассмотрим изгибаемый элемент без предварительного напряжения. В расчетной схеме усилий принимается, что на элемент действует изгибающий момент М вычисляемый при расчетных значениях нагрузок, а в арматуре и бетоне действуют усилия, определяемые при напряже­ниях, равных расчетным сопротивлениям (рисунок 7.6). В бетоне сжатой зоны криволинейную эпюру напряже­ний заменяют (для упрощения) прямоугольной, что не­значительно отражается на результатах расчета. Напря­жение в бетоне принимают одинаковым во всей сжатой зоне, равным Rb — расчетному призменному сопротив­лению на сжатие.

Рисунок 7.6. Схема усилий при расчете прочности изгибаемых элементов по нормальному сечению

 

Сечение элемента может быть любой формы, симмет­ричной относительно оси, совпадающей с силовой плос­костью изгиба. В растянутой зоне сечения элемента расположена арматура с площадью сечения As и расчетным сопротивлением на растяжение Rs. Арматура может быть также в сжатой зоне площадью сечения A’s с расчетным сопротивлением на сжатие Rsc.

На рисунке 7.6 обозначены: а — расстояние от равнодействующей усилий в арматуре As до растянутого края сечения; а' — расстояние от равнодействующей усилий в арматуре A’s до сжатого края сечения; h0 — рабочая высота сечения; Abc — площадь сечения сжатой зоны бетона; zb — расстояние между центром тяжести сжатой зоны бетона и равнодействующей усилий во всей растяну­той арматуре.

Равнодействующие усилий в арматуре и бетоне равны:

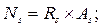
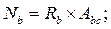
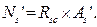(7.1)

Из условия равенства нулю суммы проекции всех нормальных усилий на ось элемента:

(7.2)

можно определить площадь сечения бетона Abc сжатой зоны, а по ней и высоту сжатой зоны х (рисунок 7.6).

Прочность элемента достаточная, если внешний расчетный изгибающий момент не превосходит расчетной несущей способности сечения, выраженной в виде обратно направленного момента внутренних сил. При моментах, взятых относительно оси, нормальной к плоскости действия изгибающего момента и проходящей через точку приложения равнодействующей усилий в растянутой арматуре As условие прочности выражается неравенством:

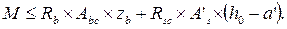(7.3)

Для высокопрочной арматуры Rs в формулах (7.1) — (7.3), умножают на дополнительный коэффициент условия работы γs6:

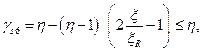(7.4)

где для А-IV η=1,20; для A-V, В-II, Bр-II, К-7 и К-19 η=1,15; для А-VI и Ат-VII η=1,10 (значения η берутся в соответствии со СНиП 2.03.01-84);

ξ— относительная высота сжатой зоны, определяемая по формуле ξ = x/h0 (при х, вычисляемом без γs6).

Рекомендуется применять изгибаемые элементы, в которых удовлетворяется условие x≤ ξR•h0 во избежание условия хрупкого разрушения.

Значение граничной относительной высоты сжатой зоны для прямоугольных, тавровых и двутавровых сече­ний определяют по формуле:

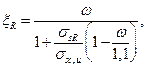(7.5)

где ω— характеристика сжатой зоны бетона, определяемая для тя­желого бетона по формуле:

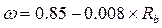(7.6)

σsR—условное напряжение в арматуре, вычисляемое для арматуры без площадки текучести (класса A-IV и выше), про­волоки В-П, Вр-II, канатов по формуле:

σsR = Rs+ 0,002 Еs = Rs + 400 (7.7)

или из равенства σsR =Rs для арматуры с площадкой текучести (классов A-I, A-II, А-III) и арматурной про­волоки (классa Вр-I), обычно не используемых для предвари­тельного напряжения. Здесь Rs — расчетное сопротивление армату­ры растяжению без учета коэффициента γs6, но с учетом других коэффициентов условий работы γsi.

Если применяется бетон с коэффициентом условий работы γb2= 1.1, в формуле (7.5) берут σsc,u= 400 МПа, если γb2=0,85-1.1, то σsc,u= 500 МПа.

При условии x>ξR•h0, установленном по равенству (7.2), допускается вычислять изгибающий момент, вы­держиваемый элементом, по условию (7.3) при значе­нии x= ξR•h0.

11. Расчет прочности по нормальным сечениям элементов прямоугольного профиля с одиночной арматурой. Элемент с прямоугольным поперечным сечением и одиночной арматурой (без предварительного напряже­ния) имеет следующие геометрические характеристики (рисунок 7.7 ):

Abc=b x; zb=h0 - 0.5 x, (7.8)

где h0 – рабочая высота сечения;

b – рабочая ширина сечения.

Высоту сжатой зоны х определяют на основании формулы (7.2) из выражения

b x Rb=Rs As (7.9)

Условие прочности, согласно выражению (7.3), име­ет вид:

M ≤ Rb b x (h0 — 0,5 x) (7.10 )

Удобно пользоваться также неравенством, принимая моменты относительно оси, проходящей через центр тя­жести сжатой зоны:

M<Rs As (h0 — 0,5x)(4.11)

Формулы (4.9) и (4.10) или (4.11) применяют совместно приx≤ ξR•h0 , гдеξR устанавливают из выражения (4.5).

Коэффициент армирования

μ =As/(bh0) (4.12)

и процент армирования μ·100 с учетом соотношений (4.9) и ξ=x/h0 могут быть представлены так:

Рисунок 4.7 – Элемент прямоугольного профиля с одиночной арматурой

и схема усилий при расчете его прочности

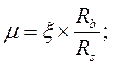
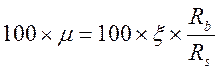(4.13)

Отсюда можно установить максимально допустимое содержание арматуры в прямоугольном сечении по пре­дельным значениям ξR, используяформулу (4.5).

Если x>ξR / h0, то изгибающий момент вычисляют по формуле (4.10) или по формуле (4.11) при x= ξR•h0 .

Из анализа выражений (4.10) и (4.11) следует, что несущая способность элемента может быть удовлет­ворена при различных сочетаниях размеров поперечного сечения элемента и количества арматуры в нем.

В реальных условиях стоимость железобетонных эле­ментов, близкая к оптимальной, получается при значе­ниях:

μ = 1...2%;ξ=0,3... 0,4 для балок;

μ = 0,3...0,6%; ξ =0,1... 0,15 для плит.

12. Элементы прямоугольного профиля с двойной армату­рой.

Железобетонные элементы с двойной арматурой.

Железобетонные балки с двойной арматурой применяют в том случае, когда изгибающий момент по длине балки меняет знак, т.е. растянутые волокна будут находиться как в верхней, так и в нижней частях балки.

 

 

 

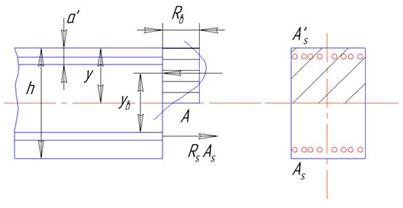
В этом случае условие прочности можно также получить из условия равенства моментов относительно точки А

,

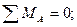
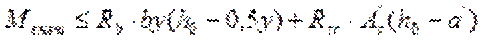где Rsc – предельное сопротивление стали арматуры сжатию;

А - площадь сечения сжатой арматуры.

Положение нейтральной оси и площадь сжатой зоны определяются из условия равенства нулю продольных сил

 

 

 

 

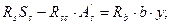
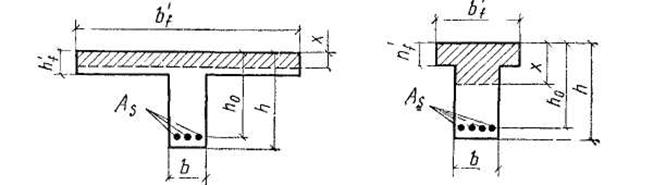
13. Расчет прочности по нормальным сечениям элементов таврового профиля. Тавровые сечения железобетонных элементов встре­чаются в практике строительства весьма часто как в от­дельных изделиях — балках (рисунок 4.8, а, б), так и в составе конструкций — в монолитных ребристых и сбор­ных панельных перекрытиях (рисунок 4.8, в, г). Тавровое сечение состоит из полки и ребра.

В сравнении с прямоугольным (пунктир на рисунке 4.8, а)тавровое сечение значительно выгоднее, так как при одной и той же несущей способности (несущая способность железобетонного элемента не зависит от площади сечения бетона

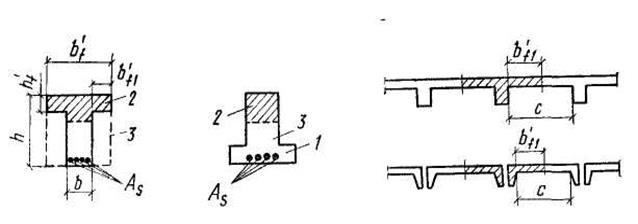
а) балка с полкой в сжатой зоне; б) то же в растянутой зоне;

в) тавро­вое сечение в составе монолитного перекрытия;

г) то же в составе сборногоперекрытия,

1 – полка; 2 – сжатая зона, 3 – ребро

Рисунок 4.8 – Тавровые сечения

растянутой зоны) бетона на не­го расходуется меньше из-за сокращенных размеров растянутой зоны. По той же причине более целесообразно тавровое сечение с полкой в сжатой зоне (рисунок 4.8, а), так как полка в растянутой зоне (рисунок 4.8, б)не повышает несущей способности элемен­та. Тавровое сечение имеет, как правило, одиночное ар­мирование.

При большой ширине полок участки свесов, более удаленные от ребра, напряжены меньше. Поэтому в рас­чет вводят эквивалентную ширину свесов полки bf1’ (рисунок 4.8, в, г). Она принимается равной: в каждую сторону от ребра — не более половины расстояния в све­ту между ребрами си не более 1/6 пролета рассчитыва­емого элемента, а в элементах с полкой толщиной h'f< 0,1hбез поперечных ребер или с ребрами при расстоя­нии между ними — больше расстояния между продоль­ными ребрами; вводимая в расчете ширина каждого свеса b’f1не должна превышать 6·h’f. Для отдельных ба­лок таврового профиля (при консольных свесах полок) вводимая в расчет ширина свеса bf1’ (рисунок 4.8, а) должна составлять:

при h’f ≥ 0.1·h ………...……………..неболее 6•h’f;

при 0,05≤ h’f<0,1·h.......................не более 3•h'f.

При h'f<0,05•hсвесы полки в расчете не учитывают.

 

При расчете тавровых сечений различают два случая для положения нижней границы сжатой зоны: в преде­лах полки (рисунок 4.9, а) и ниже полки (рисунок 4.9, б).

а) нейтральная ось проходит в пределах полки;

б) нейтральная ось проходит ниже полки

 

Рисунок 4.9 – Два расчетных случая для тавровых сечений

 

Нижняя граница сжатой зоны располагается в преде­лах полки, т. е. x ≤ h'f, в сечениях с развитыми свесами. В этом случае тавровое сечение рассчитывают как пря­моугольное с размерами b’f и h0 (рисунок 4.9, а), по­скольку площадь бетона в растянутой зоне на несущую способность не влияет.

Расчетные формулы (для элементов без предвари­тельного напряжения):

 

Rb b'f x = Rs As;(4.19)

M ≤ Rb b'f 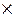(h0 - 0,5 x) (4.20)

или

M ≤ αm Rb b'f h02, (4.21)

где α m — коэффициент из таблицы 4.1

Нижняя граница сжатой зоны размещается ниже полки, т. е. x>h'n, в сечениях со слаборазвитыми свесами. В этом случае сжатая зона сечения состоит из сжа­той зоны ребра и свесов полки.

Положение нижней границы сжатой зоны определя­ется из уравнения

 

b x Rb+Rb (b’f-b) h’f=Rs As. (4.22)

Условие прочности при моментах, вычисляемых от­носительно оси, нормальной к плоскости изгиба и прохо­дящей через точку приложения равнодействующей уси­лий в растянутой арматуре, имеет вид:

M ≤ b x Rb 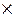(h0 - 0,5 x)+ Rb (b’f-b) h’f (h0 - 0,5 h’f). (4.23)

 

Для тавровых сечений должно соблюдаться условие x≤ ξ R•h0.

Ориентировочно высота тавровой балки может быть в пределах (из опыта проектирования)

h = (7...9) 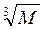,(4.24)

где h − в сантиметрах, а М − в кН·м.

Ширину ребра обычно принимают равной:

b= (0,4...0,5) h. (4.25)

Размеры полки b’f и h'fчаще всего известны из компо­новки конструкции. Сечение арматуры Asпо расчетному моменту определяют в зависимости от расчетного слу­чая. Если нейтральная ось проходит в пределах полки, то Asнаходят из расчета сечения как прямоугольного с одиночной арматурой при размерах b'fи h0, используя таблицу 4.1.

Расчетный случай таврового сечения может быть оп­ределен по следующим признакам:

1) если известны все данные о сечении, включая As, то при

Rs As ≤ Rb b’f h’f(4.26)

граница сжатой зоны проходит в полке; при обратном неравенстве она пересекает ребро;

2) если известны размеры сеченияb’f, h’f, h, bи задан расчетный изгибающий момент, но Asнеизвестно, то при

M ≤ Rb b’f h’f (h0 -0,5 h’f)(4.27)

граница сжатой зоны проходит в полке; при обратном неравенстве она пересекает ребро.

Для случая, когда граница сжатой зоны проходит ни­же полки, формулы (4.22) и (4.23) можно преобра­зовать с учетом соотношенийx= ξR•h0 и (4. 16):

Rs As= Rb (b’f-b) h’f +ξ Rb b h0(4.28)

M ≤ αm Rb b h02 + Rb (b’f-b) h’f (h0 -0,5 h’f),(4.29)

где коэффициенты ξ, αmпринимаютпо таблице 4.1.

Эти формулы можно использовать для подбора се­чения. Если требуется определить As, то из (4.29) вы­числяют

αm=[M -Rb (b’f-b) h’f (h0 -0,5 h’f)]/ (Rb b h02), (4.30)

затем из таблицы 4.1 находят ξ, соответствующее вычис­ленному αm, и, согласно формуле (4.28),

As = [ξ b h0 + (b’f-b) h’f] Rb/Rs.(4.31)

Если необходимо проверить прочность сечения при всех известных данных, то расчетный случай лучше уста­новить по формуле (4.27) и затем (если граница сжа­той зоны ниже полки) по выражению (4.22) вычислить высоту сжатой зоны х, после чего воспользоваться фор­мулой (4.23).

14. Образование наклонных трещин в ЖБ элементах обусловлено совместным действием изгибающих моментов и поперечной силы. Разрушении по наклонному сечению не менее вероятно чем по горизонтальному сечению и может происходит по одному из 3-х возможных случаев.

· раздробление бетона по накл. полосе между накл. трещинами. Возникает от главных напряжений

· Сдвиг по накл. сечению. Возникает от действия поперечных ссил.

· Излом по накл. сечению возникает от действия изгибающего момента.
12345678910Следующая ⇒

Date: 2015-09-05; view: 587; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.006 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию