
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вывод уравнения Колмогорова
|
|
Пусть имеется система S с рядом дискретных состояний S1,S2,…,Sn. Обозначим Pi(t) – вероятность того, что в момент времени система будет находится в состоянии Si. Очевидно, что для любого момента времени:
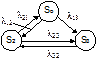 i=1∑n = Pi(t) = 1. Для определенной вероятности P1(t),P2(t),…, Pn(t) введем интенсивность перехода из состояния i в j. λij. Si → Sj. Под интенсивность перехода понимается: λij=Δt→0Lim Pij(Δt)/Δt, где Pij(Δt) - вероятность перехода системы из состояния Si → Sj за промежуток времени Δt. Вероятность перехода. Pij(Δt)=λij Δt
i=1∑n = Pi(t) = 1. Для определенной вероятности P1(t),P2(t),…, Pn(t) введем интенсивность перехода из состояния i в j. λij. Si → Sj. Под интенсивность перехода понимается: λij=Δt→0Lim Pij(Δt)/Δt, где Pij(Δt) - вероятность перехода системы из состояния Si → Sj за промежуток времени Δt. Вероятность перехода. Pij(Δt)=λij Δt
Предположим что нам известно λij для всех пар состояний Si, Sj если у стрелок на графе состояний интенсивность перехода, то это график состояния называется размеченным. Зная размеченный график состояния можно определить вероятность Рi(t) как функцию времени. Эти вероятности удовлетворяют уравнениями Колмогорова. Рассмотрим вывод уравнения Колмогорова на примере.
Р1(t+Δt)=P1(t){1-[P12(Δt)+P13(Δt)]}+P2(t)P21(Δt)
Р1(t+Δt)=P1(1){1-[λ12 Δt+ λ13Δt]}+P2(t) λ21 Δt.
Раскрыв скобки в правой части и перенеся скобки в левую часть:
dP1(t)/Δt=λ12P1(t)-λ13P1(t)+λ21 P2(t)
Аналогично рассмотрим S2 и S3 запишем дифференциальное уравнения
dP2(t)/dt=–λ21P2(t)–λ23P2(t)+λ12P1(t)+λ32P3(t)
dP3(t)/ dt = - λ32P3(t) + λ13P1(t)+ λ23P2(t)
Эти выражения для вероятности состояния называется уравнениями Колмогорова. Интегрирование системы уравнений дает искомые вероятности состояний как функций времени. Начальные условия. необходимое для интегрирования уравнений берется в зависимости от того, каким было начальное состояние системы s. Если в начальный момент времени система находится в состоянии s, то необходимо принять следующие условия при t=0. P1(t)=1, P2(t)=0, P3(t)=0
При решении следует учитывать, что все дифференциальный уравнения можно не записывать, так как для любого времени t справедливо условие.
P1(t)+P2(t)+P3(t) =1
Правило построения дифференциального уравнения. В левой части каждого уравнения стоит производная вероятность состояния, а правая часть содержит столько членов, сколько стрелок, связано с данным состоянием. Если стрелки направлены из состояния, соответствий членов имеет знак «-»,если в состоянии то «+». Каждый член равен интенсивности перехода, соответствий данной стрелки, умноженное на вероятность того состояния, из которого выходит стрелка. Это правело, дает возможность записывать дифференциальные уравнения для вероятности непосредственно размеченному графику перехода.
Следовательно обратить внимание не особенности связанные с возможной областью. Применения уравнений Колмогорова. Поэтому необходимо с понятием потока событий. Поток событие – последовательных однородных событий, следующих одно за другим в случайные моменты времени. Направление поток вызова на телефонную станцию, поток отказов в техническом устройстве. При рассмотрении процессов, протекающих в системе часто бывает удобно представить себе процесс так, как будто переходы системы из состояние в состояние происходит под действием поток событий. Поток событий обладает своими стационарностями (неизменности вероятных характеристик потока во времени, то есть вероятность появление n отказов в промежуток времени Δt зависит только от n, Δt и не зависит от положения промежутка Δt на оси времени.). Отсутствием после действия (события, образующие поток появляется в последовательные моменты времени, независимо друг о друга или когда вероятность наступления n отказов было как они распределятся до начала промежутка Δt). Ординарность – события происходящие По-одиночки, а не парами, называется простейшим потоком или стационарным Пуассоновским. Если все потоки событий, под действием которых система переходит из состояния в состояние простейшие, то случайная велечена – время пребывания системы в каждом из состояний распределяется по экспоненциальному закону. При этом случайный процесс, протекает в системе Марковский и он описывается дифференциальным уравнение Колмогорова. Уравнения Колмогорова действуют и в том случае, когда потоки не обладают своими стационарностями. Такие потоки называется нестационарными Пуассоновскими. В уравнения Колмогорова интенсивность перехода становятся функциями времени. В случаи не Пуассоновских потоков имеются специальные приемы, сводящие не Марковские потоки к Марковским. В дальнейшем будущем считать все потоки простые с постоянной интенсивностью перехода. λij = const
-------------------------------------------------------------------------------------------------------------------------------------------
Date: 2015-09-05; view: 782; Нарушение авторских прав