
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула Бернулли
|
|
Вероятность одного сложного события, состоящего в том, что в n испытаниях событие A наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна
pkqn-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. 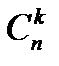 . Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события A в n испытаниях) равна вероятности одного сложного события, умноженного на их число:
. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события A в n испытаниях) равна вероятности одного сложного события, умноженного на их число: 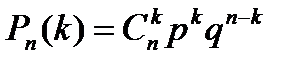 или
или  . Полученную формулу называют формулой Бернулли.
. Полученную формулу называют формулой Бернулли.
. 7. Первообразная функции, неопределенный интеграл, свойства.
Функция F(x) называется первообразной для данной функции f{x), если F'(x)=f(x), или, что то же, если dF(x)=f(x)dx.
Теорема. Если функция f(x), определенная в некотором промежутке (X) конечной или бесконечной длины, имеет одну первообразную, F(x), то она имеет и бесконечно много первообразных; все они содержатся в выражении F(x)+С, где С — произвольная постоянная.
Совокупность всех первообразных для данной функции f(x), определенной в некотором промежутке или на некотором отрезке конечной или бесконечной длины, называется неопределенным интегралом от функции f(x) [или от выражения f(x)dx ] и обозначается символом 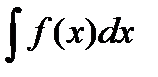 .
.
Если F(x) есть одна из первообразных для f(x), то согласно теореме о первообразных
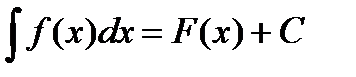 , где С есть произвольная постоянная.
, где С есть произвольная постоянная.
По определению первообразной F'(x)=f(x) и, следовательно, dF(x)=f(x) dx. В формуле (7.1), f(x) называется подинтегральной функцией, а f(x) dx — подинтегральным выражением.
Рассмотрим основные свойства неопределенного, интеграла.
1. Дифференциал от неопределенного интеграла 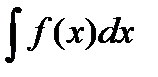 равен подинтегральному выражению f(x) dx:
равен подинтегральному выражению f(x) dx:
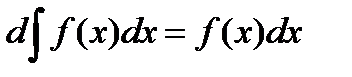 . (7.2)
. (7.2)
2. Неопределенный интеграл 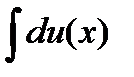 от дифференциала некоторой функции u(х) равен этой функции плюс произвольная постоянная:
от дифференциала некоторой функции u(х) равен этой функции плюс произвольная постоянная:
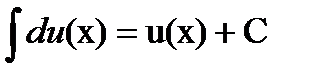 . (7.3)
. (7.3)
3. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых функций:
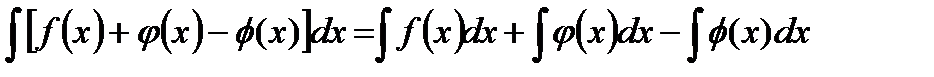 (7.4)
(7.4)
4. Постоянный множитель (отличный от нуля) можно выносить из-под знака неопределенного интеграла:
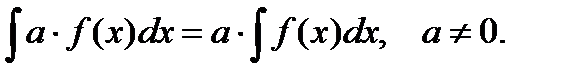 (7.5)
(7.5)
Доказательство. Левая часть равенства (7.5) есть множество А всех функций, дифференциал которых равен, согласно.
5. Если  , то
, то 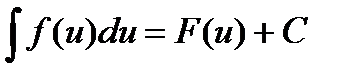 , где u(х) — произвольная дифференцируемая функция.
, где u(х) — произвольная дифференцируемая функция.
Свойство 5 есть прямое следствие свойства инвариантности дифференциала, согласно которому dF(u)—F'(u) du=f(u) du, если dF(x)=F'(x) dx=f(x) dx.
Таблица основных неопределенных интегралов.
1. 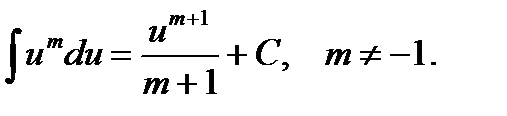 9.
9. 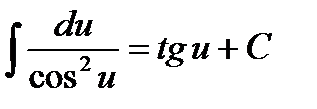
2. 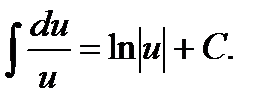 10.
10. 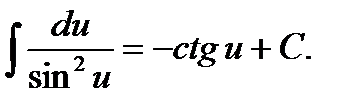
3. 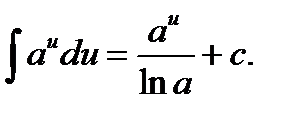 11.
11. 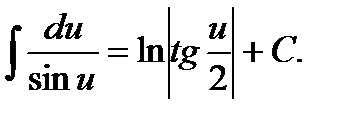
4. 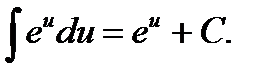 12.
12. 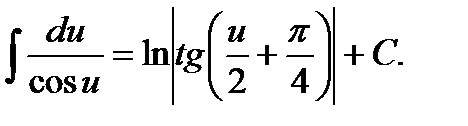
5.  13.
13. 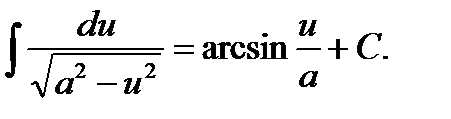
6. 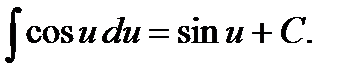 14.
14. 
7. 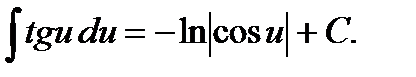 15.
15. 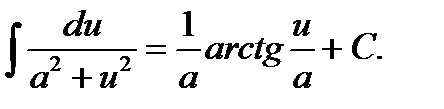
8.  16.
16. 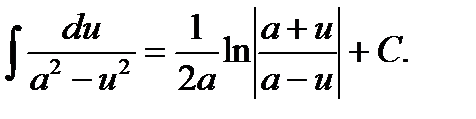
8. Методы интегрирования: непосредственное интегрирование; интегрирование подстановкой; интегрирование по частям.
Непосредственное интегрирование – это метод, основанный на применении табличных формул.
Интегрирование по частям.
Пусть и и v — две дифференцируемые функции аргумента х.
Тогда, как известно, 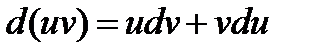 . Отсюда
. Отсюда 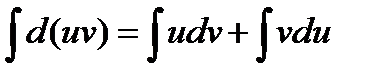 ,или
,или  . Включая произвольное постоянное слагаемое в состав одного из интегралов правой части последнего равенства, получим формулу
. Включая произвольное постоянное слагаемое в состав одного из интегралов правой части последнего равенства, получим формулу
 . (7.8)
. (7.8)
Метод интегрирования по частям заключается в следующем. Предложенный к вычислению неопределенный интеграл 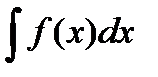 мы приводим к виду
мы приводим к виду 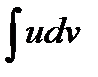 , причем так, чтобы по выражению
, причем так, чтобы по выражению 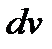 мы смогли найти первообразную функцию v (т.е. смогли бы проинтегрировать выражение dv); заметим, что здесь нам достаточно найти какую-нибудь одну из первообразных.
мы смогли найти первообразную функцию v (т.е. смогли бы проинтегрировать выражение dv); заметим, что здесь нам достаточно найти какую-нибудь одну из первообразных.
После этого применяем к нашему интегралу 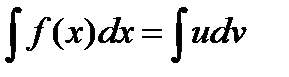 формулу (7.8) в предположении, что вычисление интеграла
формулу (7.8) в предположении, что вычисление интеграла 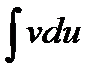 окажется проще, чем вычисление интеграла
окажется проще, чем вычисление интеграла 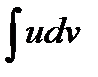 , или что
, или что 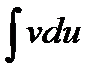 окажется подобным интегралу
окажется подобным интегралу 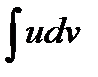 (с коэффициентом, отличным от единицы). Заметим при этом, что для получения окончательного результата может иной раз потребоваться применение метода интегрирования по частям последовательно несколько раз.
(с коэффициентом, отличным от единицы). Заметим при этом, что для получения окончательного результата может иной раз потребоваться применение метода интегрирования по частям последовательно несколько раз.
Интегрирование подстановкой.
Метод заключается в преобразовании аргумента подынтегральной функции по некоторой формуле, рассчитанной на то, чтобы интеграл в новой переменной оказался проще для вычисления.
Итак, пусть для вычисления неопределенного интеграла  от непрерывной функции f{x) произведена подстановка:
от непрерывной функции f{x) произведена подстановка: 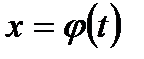 , где функция
, где функция 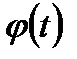 монотонная и имеет непрерывную производную; обозначим через
монотонная и имеет непрерывную производную; обозначим через 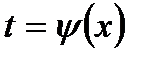 обратную функцию, существование и непрерывность которой следуют из предположенной нами монотонности и непрерывности подстановочной функции
обратную функцию, существование и непрерывность которой следуют из предположенной нами монотонности и непрерывности подстановочной функции 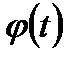 . В силу нашей подстановки
. В силу нашей подстановки 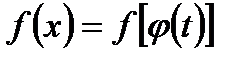 ,
, 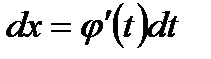 . Заменяя f(x) и dx их новыми выражениями, мы приводим исходный интеграл к виду
. Заменяя f(x) и dx их новыми выражениями, мы приводим исходный интеграл к виду 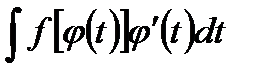 , где
, где 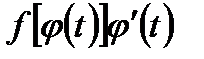 есть непрерывная функция аргумента t.
есть непрерывная функция аргумента t.
Докажем, что новый интеграл будет равен исходному:
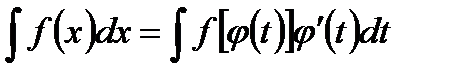 t. (7.9)
t. (7.9)
Для этого нам достаточно будет доказать совпадение дифференциалов от левой и от правой части равенства (7.9) при 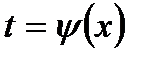 , или, что то же, при
, или, что то же, при 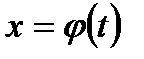 . Имеем
. Имеем
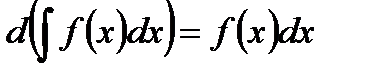 ,
, 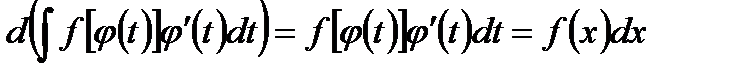 ,
,
поскольку 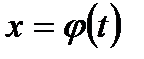 . Равенство (7.9) доказано.
. Равенство (7.9) доказано.
Равенство (7.9) является рабочей формулой для вычисления интегралов методом подстановки (преобразования переменной). После вычисления интеграла, стоящего в правой части формулы, надо еще заменить в его выражении t на 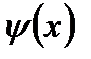 (используя функцию, обратную к подстановочной) с тем, чтобы вернуться к первоначальной переменной х.
(используя функцию, обратную к подстановочной) с тем, чтобы вернуться к первоначальной переменной х.
10. Линейное однородное дифференциальное уравнение 1-ого порядка, вывод его решения.
Уравнение вида 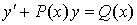 ,(4) где Р(х) и Q(x) непрерывные функции от х, называется линейным.
,(4) где Р(х) и Q(x) непрерывные функции от х, называется линейным.
Для решения уравнения (4) при 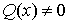 применим метод Бернулли. Будем искать неизвестную функцию
применим метод Бернулли. Будем искать неизвестную функцию 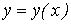 в виде произведения двух пока неизвестных функций от х, т.е. положим
в виде произведения двух пока неизвестных функций от х, т.е. положим
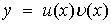 , тогда
, тогда  . Подставляем выражения y и
. Подставляем выражения y и 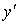 в (4) имеем:
в (4) имеем: 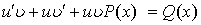 , или
, или 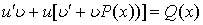 (5)
(5)
Так как искомое решение у – есть произведение двух функций, то одна из них может быть выбрана произвольно, другая же должна определятся уравнением (5). Выберем функцию 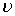 (x) так, чтобы выражение, стоящее в скобках, обращалось в нуль, т.е.
(x) так, чтобы выражение, стоящее в скобках, обращалось в нуль, т.е. 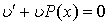 .
.
Для этого достаточно, чтобы 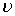 (x) было каким-либо частным решением уравнения с разделяющимися переменными:
(x) было каким-либо частным решением уравнения с разделяющимися переменными:
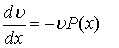 .
.
Решая его находим 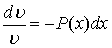 ,
,  ,
, 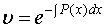 .
.
Подставляя найденную функцию 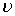 в уравнение (5) имеем уравнение с разделяющимися переменными
в уравнение (5) имеем уравнение с разделяющимися переменными
 ,
, 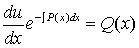 ,
, 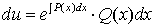 ,
, 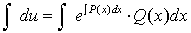 ,
, 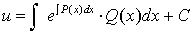 .
.
Тогда искомое решение линейного дифференциального уравнения будет иметь вид
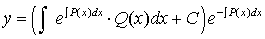 .
.
Иногда дифференциальное уравнение первого порядка является линейным не относительно у, а относительно х, т.е. может быть приведено к виду 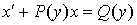 . Метод интегрирования тот же, только в этом случае полагаем
. Метод интегрирования тот же, только в этом случае полагаем
 , т.е. у - аргумент, а х - функция
, т.е. у - аргумент, а х - функция 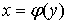 .
.
11. Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, и структура его решения.
Пусть имеем линейное однородное уравнение 2-го порядка  , (1) где p, q – постоянные действительные числа.
, (1) где p, q – постоянные действительные числа.
Чтобы найти общий интеграл этого уравнения, достаточно найти два линейно независимых частных решения. Будем искать решения в виде 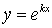 где
где 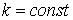 , (2) тогда
, (2) тогда 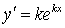 ,
,  .
.
Подставляя найденные значения  ,
, 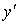 ,
,  в уравнение (1), получим
в уравнение (1), получим
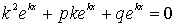 ,
, 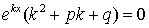 .
.
Отсюда, так как 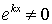 , то
, то 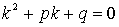 . (3)
. (3)
Очевидно, что если  будет удовлетворять уравнению (3), то
будет удовлетворять уравнению (3), то 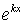 будет искомым решением уравнения (1). Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1).
будет искомым решением уравнения (1). Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1).
Характеристическое уравнение есть квадратное уравнение, имеющее два корня: обозначим их через k1 и k2. При этом возможны в зависимости от значения 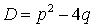 следующие случаи:
следующие случаи:
1) если D>0, то k1,k2 – действительные и при том не равные между собой числа:  ;
;
2) если D=0 то k1,k2 действительные, равные числа 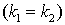 ;
;
3) если D<0, то k1,k2 – комплексные числа 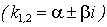 .
.
Рассмотрим отдельно каждый случай.
1) корни характеристического уравнения действительны и различны:  . В этом случае частными решениями будут функции
. В этом случае частными решениями будут функции 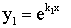 ,
,  . Тогда общее решение уравнения (1) имеет вид
. Тогда общее решение уравнения (1) имеет вид 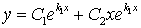 , где C1 и C2 – некоторые числа.
, где C1 и C2 – некоторые числа.
2) если корни характеристического уравнения действительные и равные. В этом случае k1=k2, то общее решение имеет вид 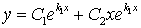 .
.
3) если характеристическое уравнение не имеет действительных корней, то общее решение уравнения имеет вид
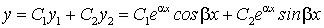 или
или 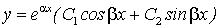 ,
,
где С1 и С2- произвольные числа; 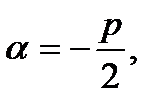
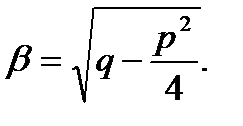
Date: 2015-09-05; view: 395; Нарушение авторских прав