
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нормальное уравнение плоскости в векторной и координатной формах (вывод)
|
|
|
|
|
|
|
|
|
|
Положение плоскости в трехмерном пространстве будет вполне определено, если известно ее расстояние P от начала координат O, т.е. длина перпендикуляра ON, опущенного из точки O на плоскость, и единичный вектор
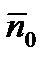 , перпендикулярный к плоскости. По условию,
, перпендикулярный к плоскости. По условию, 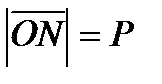 . Для любой точки M(x,y,z), лежащей на плоскости, имеем:
. Для любой точки M(x,y,z), лежащей на плоскости, имеем:
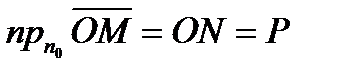
С другой стороны, по определению скалярного произведения двух векторов имеем:
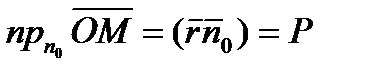 или
или
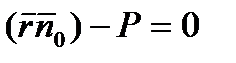 (1)
(1)
Уравнение (1) называется векторным уравнением плоскости. Одновременно уравнение (1) называется нормальным уравнением плоскости.
Пусть теперь единичный вектор 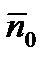 образует с осями координат соответственно углы α, β, γ. Тогда
образует с осями координат соответственно углы α, β, γ. Тогда 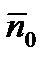 имеет своими координатами направляющие косинусы, т.е.
имеет своими координатами направляющие косинусы, т.е. 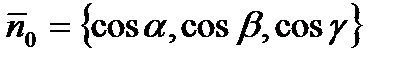 . Далее, вектор
. Далее, вектор  . Тогда получим скалярное произведение векторов:
. Тогда получим скалярное произведение векторов:
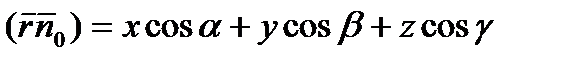
При этом уравнение (1) примет вид:
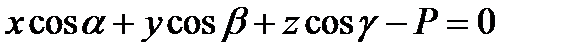 (2)
(2)
Уравнение (1) называется нормальным (нормированным) уравнением плоскости в координатной форме.
Замечание: как и в случае нормального уравнения прямой, в рассматриваемом случае уравнение (2) можно получить, используя теорию проекций.
2. Общее уравнение плоскости Уравнение плоскости в отрезках.
|
|
|
|
|
|
|
|
|
|
Пусть плоскость не проходит через начало координат, а отсекает от осей координат соответственно отрезки a, b, c. Как видно из рисунка, плоскость проходит через точки M(a,0,0), N(0,b,0) и R(0,0,c). Пусть общее уравнение плоскости имеет вид: Ax + By + Cz + D = 0 (1). Подставим в это уравнение координаты точек M, N и R, получим:
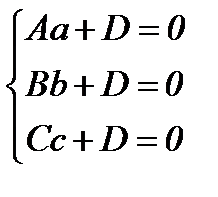 (2)
(2)
Так как плоскость не проходит через начало координат, то D≠ 0. Так как плоскость отсекает от осей координат ненулевые отрезки, то A≠ 0, B≠ 0, C≠ 0. Тогда из (2) имеем: 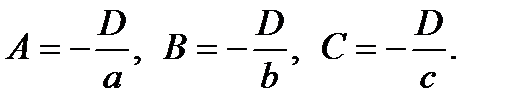
Подставив эти значения в уравнение (1), получим: 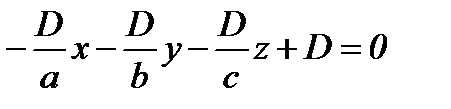 .
.
Так как D≠0, то все члены последнего равенства можно разделить на (-D). Получим:
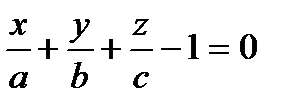 или
или  (3)
(3)
Уравнение (3) и есть уравнение плоскости в отрезках.
3. Теоремы о пределах (вывод одной из них).
Теорема 1. Для того, чтобы число A было пределом функции f(x) при x®a, необходимо и достаточно, чтобы эта функция была представлена в виде: f(x) = A+a(x), где a(x) – бесконечно малая функция.
Теорема 2. Предел постоянной величины равен самой постоянной.
Теорема 3. Если функция 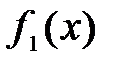 ³0 (
³0 (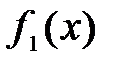 £0) для любых х в некоторой окрестности точки а, кроме быть может самой точки а, и в точке а имеет предел, то
£0) для любых х в некоторой окрестности точки а, кроме быть может самой точки а, и в точке а имеет предел, то 
Теорема 4. Если функции 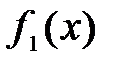 и
и 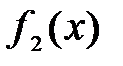 имеют пределы при x®a, то при x®a имеют пределы их сумма
имеют пределы при x®a, то при x®a имеют пределы их сумма 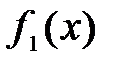 +
+ 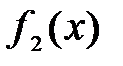 произведение
произведение 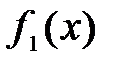
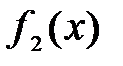 и при условии, то
и при условии, то 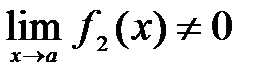 частное
частное 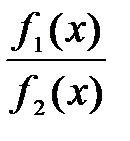 причем
причем 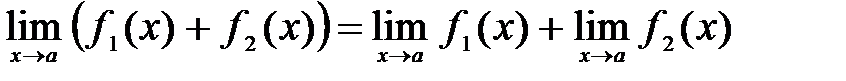 (1)
(1)
 (2)
(2)
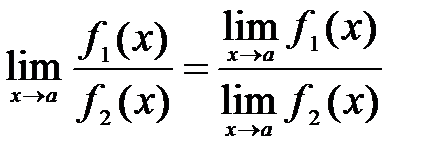 (3)
(3)
Доказательство. Ограничимся доказательством формулы (1).
Пусть 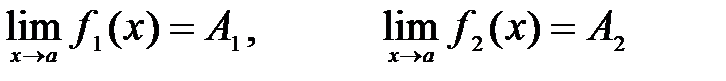 , тогда по теореме 1:
, тогда по теореме 1:
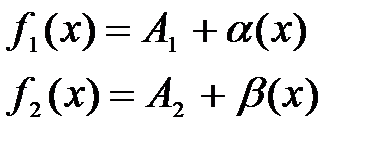 где
где 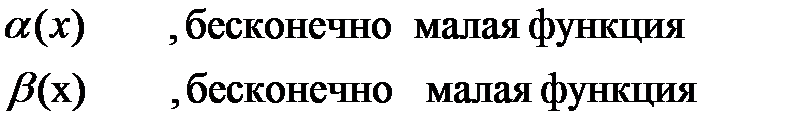
Отсюда 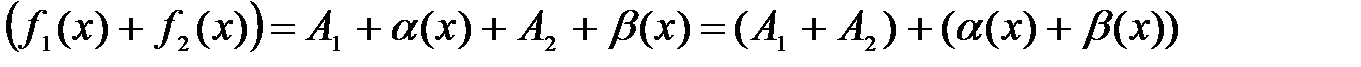
По свойству бесконечно малых (1) α(x) + β(x) – бесконечно малая, следовательно, по теореме (1):
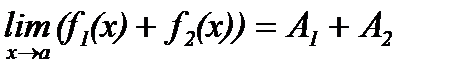 .
.
Следствие 1. Если функция f(x) имеет предел при x → a, то:
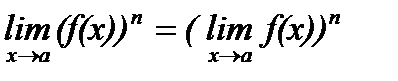 , где n – натуральное число.
, где n – натуральное число.
Следствие 2. Постоянный множитель можно выносить за знак предела:
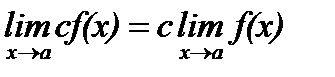 , c = const.
, c = const.
Теорема 5. Если для функций f(x), f1(x) и f2(x) в некоторой окружности точки a выполняется неравенство
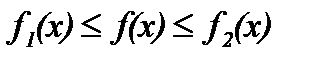 , и
, и 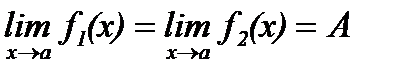 , то
, то  .
.
|
|
|
|
|
|
|
|
|
4.Первый замечательный предел (вывод).
Теорема. 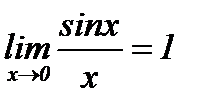 (раскрывает неопределенность типа
(раскрывает неопределенность типа 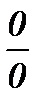 ). Доказательство. Возьмем круг единичного радиуса и положим
). Доказательство. Возьмем круг единичного радиуса и положим  . X – угол выраженный в радианах.
. X – угол выраженный в радианах.
Обозначим площади треугольника ОАВ через– S1, треугольника ОАС – S2, площадь сектора ОАВ – через S.
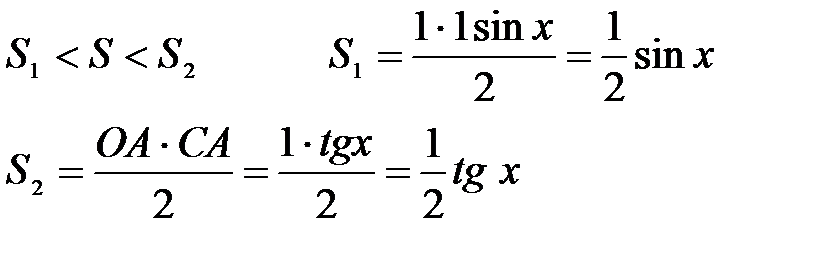
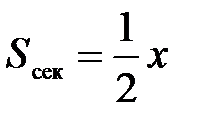

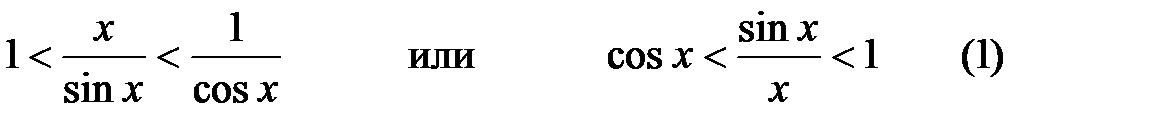
Неравенство (1) получено для 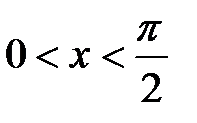 однако cos x и
однако cos x и 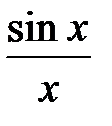 функции четные,т.к. cos (-x) = cos x.
функции четные,т.к. cos (-x) = cos x.
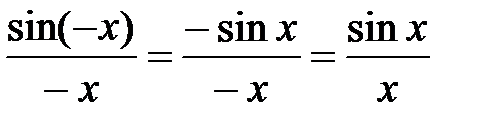 т.е. (1) справедливо и для
т.е. (1) справедливо и для 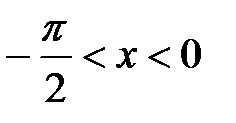 т.к.
т.к.  , то из (1) на основании теоремы 5 заключаем
, то из (1) на основании теоремы 5 заключаем 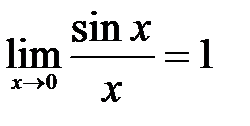 .
.
5. Производные элементарных функций (вывод одной из них).
| I. Правила дифференцирования | II. Формулы дифференцирования |
1. 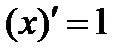 2.
2. 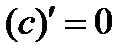 3.
3. 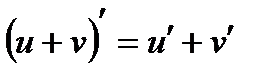
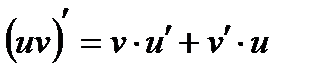
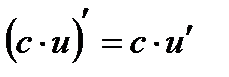
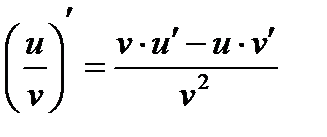
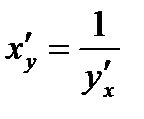
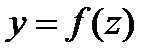 , , 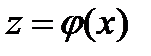 : : 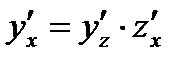
| 1. 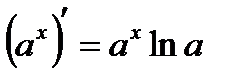 ; ; 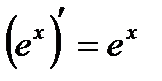 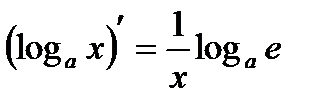 ; ; 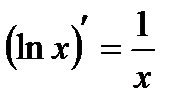 2.
2. 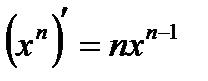 3.
3. 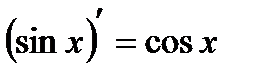 ; ; 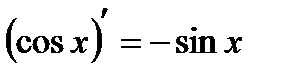 4.
4. 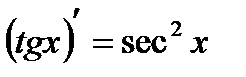 ; ; 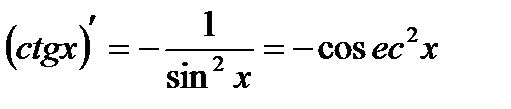 5.
5. 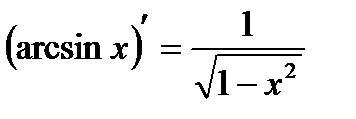 ; ; 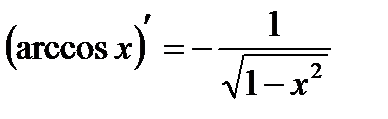 6.
6.  ; ; 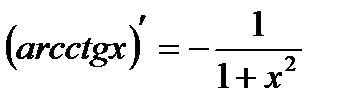
|
Выведем формулу нахождения производной показательной функции 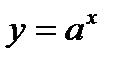
Придавая аргументу  приращение
приращение 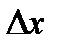 , находим для приращения функции
, находим для приращения функции 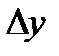 следующее значение:
следующее значение:
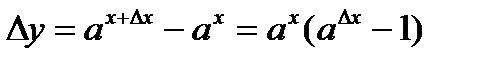 (1). Делим на
(1). Делим на 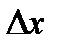 :
: 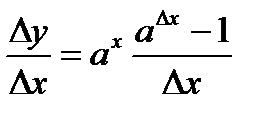 (2)
(2)
Переходим к пределу при 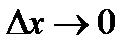 :
:
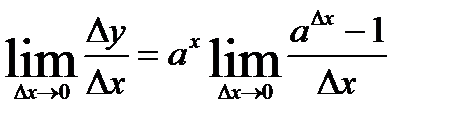 , но
, но 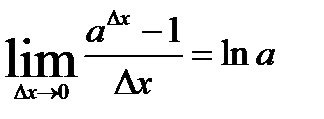 . Поэтому
. Поэтому 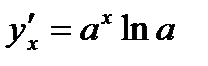 (3). Итак
(3). Итак
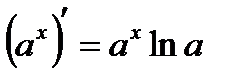 (4). В частности,
(4). В частности, 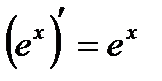 (5) (так как
(5) (так как 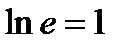 ).
).
Date: 2015-09-05; view: 852; Нарушение авторских прав