Упругие столкновения

Столкновение называется абсолютно упругим, если по завершении его тела полностью восстанавливают свою первоначальную форму и в их внутреннем состоянии не происходит каких-либо изменений, если сохраняется суммарная механическая энергия тел.

Столкновение обычных макроскопических тел в реальных условиях всегда бывают в той или иной степени неупругими, ибо они сопровождаются нагреванием тел, возникновением акустических волн и т.д., то есть превращением части механической энергии тел в другие виды энергии. Однако в некоторых случаях столкновение макроскопических тел можно с достаточной степенью точности считать абсолютно упругими (например, столкновение шаров из слоновой кости или закаленной стали). Особо важную роль упругие столкновения играют в физике атомных явлений. Так столкновение молекул газа друг с другом и со стенками сосуда, в который газ заключен, можно уподобить соударениям абсолютно упругих шаров. Упруго рассеиваются 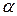- частицы при прохождении через тонкие пленки вещества (опыт Резерфорда), рентгеновские кванты при взаимодействии с электронами и т.д.

Рассмотрим абсолютно упругое центральное столкновение двух шаров с массам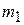и и 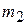. Пусть шары движутся один за другим, (первый шар догоняет второй) и перед столкновением имеют скорост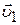и и 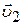соответственно. Во время столкновения шары деформируются, силы упругой деформации изменяют скорости шаров. Обозначим скорости шаров после столкновения 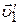и 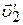. Полагая, что шары образуют замкнутую систему, применим к ним закон сохранения импульса:

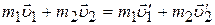(2.1)

Пусть массы шаров таковы, что и после соударения они продолжают двигаться в том же направлении, в каком двигались до столкновения. Тогда соотношение (2.1) в проекциях запишется так:

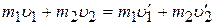(2.1,а)

Детальный анализ деформации шаров в процессе упругого столкновения весьма сложен. Но этот анализ, в принципе, и не нужен. Так как шары полностью восстанавливают свою первоначальную форму, и в их внутреннем состоянии не происходит изменений, то закон сохранения энергии сводится к сохранению кинетической энергии:

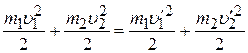(2.2)

Решая уравнения (2.1а) и (2.2) совместно (это следует проделать самостоятельно), получаем:

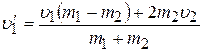(2.3)

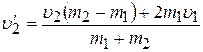(2.4)

Рассмотрим некоторые частные случаи:

а) Массы шаров равны: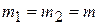

Тогда 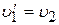и 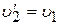. Шары просто обмениваются своими скоростями. Если до столкновения второй шар покоился 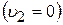, то после столкновения он начинает двигаться со скоростью первого шара (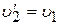), а первый шар останавливается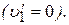

б) Масса второго шара значительно больше массы первого 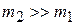. Разделим числитель и знаменатель в выражениях (2.3) и (2.4) на :

;

.

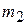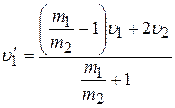В этих формулах отношением 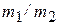в силу его малости можно пренебречь. Тогда

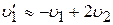
и

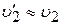
Вывод: при упругом центральном столкновении шара малой массы с шаром большой массы скорость шара большей массы практически не изменяется. Если до удара массивный шар покоился (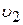 = 0), то шар малой массы отскакивает от массивного неподвижного шара со скоростью, почти равной по величине и противоположной по направлению той скорости, с которой он двигался до соударения 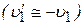. При этом легкий шар практически не передает свою кинетическую энергию массивному шару.

Полученный вывод можно применить к упругому удару шара о неподвижную стенку, перпендикулярную направлению движения шара (с этим случаем мы сталкиваемся, например, при расчете давления, оказываемого молекулами газа на стенки сосуда). Найдем приращение импульса шара при таком упругом столкновении:

.

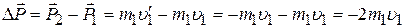Такой же по величине, но противоположный по знаку импульс, получит стенка.

в) 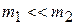, но . Шары двигаются в одном направлении. Тогда:

.

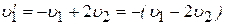В этом случае малый шар отскакивает от большого со скоростью, меньшей первоначальной на величину .

Нечто подобное происходит в цилиндре с газом при расширении газа. Молекулы, ударяющиеся о удаляющийся поршень, теряют свою скорость и, следовательно, кинетическую энергию. Эти «потери» проявляются в охлаждении газа.

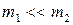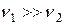г) , но .Шары двигаются навстречу друг другу. Тогда:

,

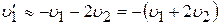т.е. проекция скорости 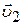на положительно выбранное направление отрицательна. В рассматриваемом случае малый шар отскакивает от большого со скоростью, превышающей ту, с которой он ударяется о большой шар на величину .

Нечто подобное происходит в цилиндре с газом при сжатии газа. Молекулы, ударяющиеся в надвигающийся поршень, увеличивают свою скорость и кинетическую энергию, что проявляется в нагревании газа.

Мы убедились, что, используя законы сохранения импульса и энергии, можно довольно просто определить скорости шаров после удара при известных величинах масс шаров и их скоростей до удара. Наоборот, зная массы шаров и их скорости до и после столкновения, легко проверить основные законы сохранения.

Рассмотрим случай, когда один из шаров (пусть это будет шар с массой 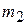) до столкновения покоился, а другой с массой 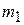обладает скоростью 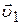. Начальные скорости шаров после столкновения обозначим соответственно 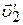и 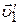. В силу законов сохранения импульса и энергии приходим к уравнениям:

(3.1)

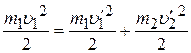. (3.2)

При центральном ударе движение столкнувшихся шаров после удара будет происходить вдоль той же прямой и в уравнении (3.1) векторные значки можно снять

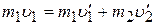(3.3)

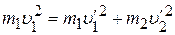(3.4)

или

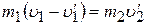(3.5)

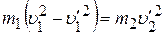. (3.6)

Разделив последнее из этих уравнений на предыдущее, находим

,

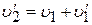и, подставляя значение 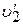в уравнение (3.5), определим скорость налетающей частицы после столкновения через ее скорость до столкновения:

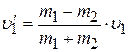(3.7)

Теперь нетрудно найти отношение кинетических энергий шаров после и до столкновения:

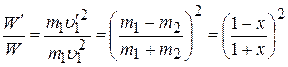, (3.8)

где через 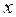обозначено отношение масс шаров .

Отсюда следует, что шар ‑ снаряд при столкновении с другим шаром замедляется тем сильнее, чем ближе между собой массы шаров. Из условия (3.3) также следует, что при 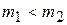, 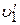< 0, то есть после столкновения с более тяжелым шаром, шар-снаряд приобретает скорость, направление которой противоположно первоначальной.

Date: 2015-09-05; view: 343; Нарушение авторских прав