Дифференциал функций и его применение для приближённых вычислений

Дифференциалом функции 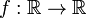в точке 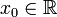называют линейную функцию 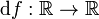, d f (x ₀)(h) = f '(x ₀) h, такую, что выполняется условие

f (x ₀ + h) − f (x ₀) = d f (x ₀)(h) + o (h ²).

Если дифференциал функции f в точке x ₀ существует, то f называется дифференцируемой в точке x ₀, а число f '(x ₀) называется производной функции f в точке x ₀. Часто дифференциал обозначают как 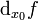или, если он подразумевается определенным на всем 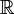, просто d f.

Заметим, что дифференциал тождественной функции имеет вид d x (h) = h, поэтому формулу дифференциала произвольной функции f можно записывать также как

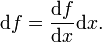
Аналогично, дифференциалом функции 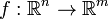в точке 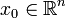называют линейный оператор 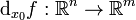такой, что выполняется условие

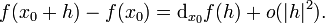
Если дифференциал функции f существует в точке x ₀, то говорят, что функция f дифференцируема в точке x ₀. Матрица этого линейного оператора называется матрицой Якоби, ее элементы будут частными производными f. Отметим, что даже если f не дифференцируема в точке x ₀, некоторые (или даже все!) ее частные производные могут в этой точке существовать; дифференцируемость эквивалентна существованию всех частных производных только в случае n = 1.

В случае m = 1 можно рассмотреть функции 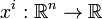, , где t стоит на i -м месте. Тогда дифференциал произвольной функции 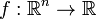, аналогично со случаем одной переменной, можно записать как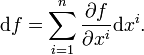

В случае m > 1 дифференциал часто называют (полной) производной функции, в этом случае его иногда обозначают как .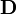

ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ

Пусть нам известно значение функции y ₀ =f(x ₀ ) и ее производной y ₀ ' = f '(x ₀) в точке x ₀. Покажем, как найти значение функции в некоторой близкой точке x.

Как мы уже выяснили приращение функции Δ y можно представить в виде суммы Δ y = dy +α·Δ x, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δ x вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δ y ≈ dy или Δ y» f '(x ₀)·Δ x.

Т.к., по определению, Δ y = f (x) – f (x ₀), то f(x) – f(x ₀ ) ≈ f '(x ₀)·Δ x.

Откуда

Date: 2015-09-05; view: 463; Нарушение авторских прав