
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрический смысл производной
|
|
Пусть 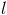 – некоторая кривая,
– некоторая кривая,  – точка на кривой
– точка на кривой 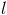 .
.
Любая прямая, пересекающая 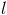 не менее чем в двух точках называется секущей.
не менее чем в двух точках называется секущей.
Касательной к кривой 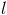 в точке
в точке  называется предельное положение секущей
называется предельное положение секущей 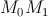 , если точка
, если точка 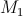 стремится к
стремится к  , двигаясь по кривой.
, двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке  существует, то она единственная
существует, то она единственная
Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке 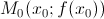 он имеет невертикальную касательную
он имеет невертикальную касательную 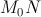 . Ее уравнение:
. Ее уравнение: 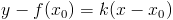 (уравнение прямой, проходящей через точку
(уравнение прямой, проходящей через точку 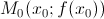 и имеющую угловой коэффициент k).
и имеющую угловой коэффициент k).
По определению углового коэффициента 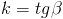 , где
, где 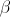 – угол наклона прямой
– угол наклона прямой 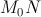 к оси
к оси  .
.
Пусть 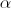 – угол наклона секущей
– угол наклона секущей 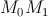 к оси
к оси  , где
, где  . Так как
. Так как 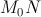 – касательная, то при
– касательная, то при 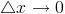
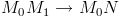 ⇒
⇒ 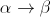 ⇒
⇒  .
.
Следовательно,
.
Таким образом, получили, что 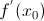 – угловой коэффициент касательной к графику функции y = f(x) в точке
– угловой коэффициент касательной к графику функции y = f(x) в точке 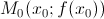 (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке
(геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке 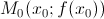 можно записать в виде
можно записать в виде
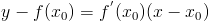
Замечание. Прямая, проходящая через точку  перпендикулярно касательной, проведенной к кривой в точке
перпендикулярно касательной, проведенной к кривой в точке  , называется нормалью к кривой в точке
, называется нормалью к кривой в точке  . Так как угловые коэффициенты перпендикулярных прямых связаны соотношением
. Так как угловые коэффициенты перпендикулярных прямых связаны соотношением 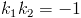 , то уравнение нормали к кривой y = f(x) в точке
, то уравнение нормали к кривой y = f(x) в точке 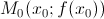 будет иметь вид
будет иметь вид
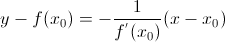 , если
, если 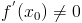 .
.
Если же 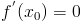 , то касательная к кривой y = f(x) в точке
, то касательная к кривой y = f(x) в точке 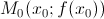 будет иметь вид
будет иметь вид 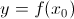 , а нормаль
, а нормаль 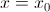
Производные от элементарных функций. Таблица производных.

| |
| 2. | 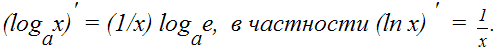
|
| 3. | 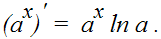
|
| 4. | 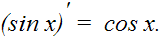
|
| 5. | 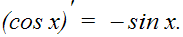
|
| 6. | 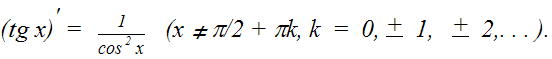
|
| 7. | 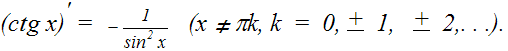
|
| 8. | 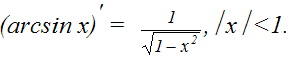
|
| 9. | 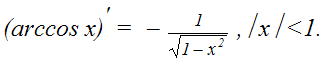
|
| 10. | 
|
| 11. | 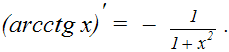
|
Производные элементарных функций
| Функция y = f (x) | Производные элементарных функций простого аргумента | Функция y = f (kx +b) | Производные элементарных функций сложного аргумента |
| y = xn | y  = n = n  xn −1 xn −1
| y =(kx + b) n | y  = n = n  k k  (kx + b) n −1 (kx + b) n −1
|
| y = x | y  =1 =1
| y =(kx + b) | y  = k = k
|
y = 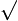 x x
| y  =12 =12 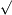 x x
| y = 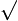 kx + b kx + b
| y  = k = k  12 12 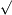 kx + b kx + b
|
| y =1 x | y  =−1 x 2 =−1 x 2
| y =1 kx + b | y  =− k =− k  1(kx + b)2 1(kx + b)2
|
| y = cos x | y  =− sinx =− sinx
| y = cos (kx +b) | y  =− ksin (kx + b) =− ksin (kx + b)
|
| y = sin x | y  = cosx = cosx
| y = sin (kx +b) | y  = kcos (kx + b) = kcos (kx + b)
|
| y = tg x | y  =1 cos 2 x =1 cos 2 x
| y = tg (kx +b) | y  = k = k  1 cos 2(kx + b) 1 cos 2(kx + b)
|
| y = ctg x | y  =−1 sin 2 x =−1 sin 2 x
| y = ctg (kx +b) | y  =− k =− k  1 sin 2(kx + b) 1 sin 2(kx + b)
|
| y = arcsin x | y  =1 =1 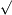 1− x 2 1− x 2
| y = arcsin (kx +b) | y  = k = k  1 1 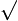 1−(kx + b)2 1−(kx + b)2
|
| y = arccos x | y  =−1 =−1 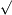 1− x 2 1− x 2
| y = arccos (kx +b) | y  =− k =− k  1 1 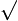 1−(kx + b)2 1−(kx + b)2
|
| y = arctg x | y  =11+ x 2 =11+ x 2
| y = arctg (kx +b) | y  = k = k  11+(kx + b)2 11+(kx + b)2
|
| y = arcctg x | y  =−11+ x 2 =−11+ x 2
| y = arcctg (kx +b) | y  =− k =− k  11+(kx + b)2 11+(kx + b)2
|
y = ax  a a 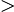 0 0  a a 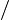 =1 =1
| y  = ax = ax  lna lna  a a 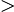 0 0  a a 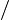 =1 =1
| y = akx + b  a a 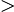 0 0  a a 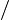 =1 =1
| y  = k = k  akx + b akx + b  lna lna  a a 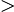 0 0  a a 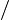 =1 =1
|
| y = ex | y  = ex = ex
| y = ekx + b | y  = k = k  ekx + b ekx + b
|
y = logax  a a 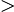 0 0  a a 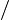 =1 =1
| y  =1 x =1 x  lna lna
| y = loga (kx + b)  a a 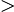 0 0  a a 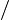 =1 =1
| y  = k = k  1(kx + b) 1(kx + b)  lna lna
|
| y = lnx | y  =1 x =1 x  x x 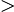 0 0
| y = ln (kx +b) | y  = k = k  1 kx + b 1 kx + b  kx + b kx + b 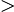 0 0
|
Date: 2015-09-05; view: 535; Нарушение авторских прав