Основная модель управления запасами

Основной моделью называется статическая однономенклатурная динамическая модель без дефицита.

Простейшая однономенклатурная модель оптимальной поставки строится при следующих предположениях:

1. Спрос в единицу времени остается постоянным;

2. Заказанная партия доставляется одновременно;

3. Дефицит не допустим;

4. Затраты на организацию поставки 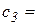const и не зависит от величины 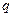партии;

5. Издержки содержания единицы продукции в течение единицы времени составляют .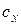

Рисунок 2. иллюстрирует статическую однономенклатурную модель без дефицита. Уровень запасов снижается равномерно от q до 0, после чего заказывается новая партия величиной q, причем заказ выполняется мгновенно.

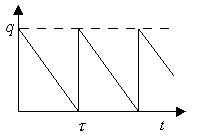
Рис. 2. Однономенклатурная модель.

Интервал времени между поставками называется циклом. Издержки в течение цикла L состоят из стоимости заказа 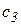и затрат на содержание запаса, которые пропорциональны средней величине запаса и длине цикла .

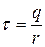(8.1)

Разделив это выражение на длину цикла, получим, издержки в единицу времени:

. (8.2)

Оптимальный размер партии определяет из уравнения:

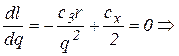
. (8.3).

Формула (2) называется формулой наиболее экономной величины заказа или формулой Уилсона.

Найдем оптимальные параметры системы:

1. Оптимальная стратегия предусматривает заказ партии товара через время, равное длине цикла:

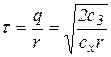. (8.4)

2. Наименьшие суммарные затраты работы системы в единицу времени:

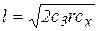(8.5)

Date: 2015-09-20; view: 609; Нарушение авторских прав