Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Постановка задачи управления запасами
|
|
Методические указания к проведению лекционного занятия
Тема № 9.6. Математическая теория оптимального управления
План:
1. Постановка задачи управления запасами
2. Основная модель управления запасами
3. Модель с конечной интенсивностью поставок
4. Модель с ограничением на емкость склада
Постановка задачи управления запасами
Предметом теории управления запасами является определение такой организации поставок или производства, при которой суммарные затраты на функционирование системы были бы минимальными. Под организацией поставок понимается определение объемов поставок и периодичность заказов, а при планировании производства нескольких видов продукции на одном и том же оборудовании – определение размера партии и периодичность запуска продукции в производство. Чем меньше запас, тем меньше издержки хранения (арендная плата), но при этом больше издержки заказа (транспортировка материалов). Кроме того, возрастает риск сбоя производства из-за задержек в поставках. Аналогично – для производимой продукции: при производстве мелких партий, издержки хранения готовой продукции минимальны, но возрастают издержки переналадки оборудования.
Возможный уровень запасов на складе предприятия можно представить графически (рис. 1):
 |
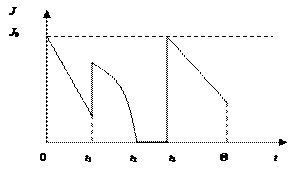Рис. 1. Модель уровня запасов на складе
где:
J – уровень запасов, являющийся функцией времени t;
J 0 – начальный уровень запасов в момент времени t= 0;
t 1, t 3 – моменты поставки новых запасов на склад;
(t 2, t 3) – интервал, в течение которого запасы на складе отсутствуют (дефицит запасов);
Θ – общий интервал времени работы по принятой модели.
Из графика на рис. 1. можно сделать вывод о существующих издержках по принятой модели. Существует 4 вида затрат, которые могут оказать влияние на выбор решения по управлению запасами:
• Затраты на приобретение запасов (следует учитывать если цена единицы продукции зависит от величины партии заказа)
• Затраты на организацию заказа (расходы на командировки, почтово-телеграфные и транспортные расходы, не зависящие от размера партии заказа)
• Издержки хранения запасов (издержки от физического присутствия запасов на складе и потери от иммобилизации средств в запасах)
• Потери от дефицита (суммарные прибыли в расчете на одну денежную единицу стоимости дефицитных материалов, обусловлены отсутствием запасов, вызывающим простой оборудования, неритмичность производства и т.д.)
При анализе запасов используются те модели управления запасами, которые наиболее точно соответствуют характеристикам исследуемого склада. Во многом модель определяется типом спроса на запасаемый продукт, который может быть детерминированным и случайным. В связи с этим выделяют детерминированные и стохастические модели.
Тип модели также существенно зависит от номенклатуры хранимых на складе изделий. Если таких изделий несколько, то модель называется многономенклатурной.
Если все параметры модели не изменяются во времени, то она называется статической, если изменяются – динамической.
В качестве критерия эффективности управления запасами принимают минимум функции затрат, представляющей суммарные затраты на хранение, поставку и дефицит запасаемого продукта.
Используя уровень запасов на складе, представленный на рис. 8.1, можно оценить затраты на хранение запаса:
Если v – затраты на хранение одной единицы продукции, а количество единиц продукции на складе в произвольный момент времени равно J (t), то стоимость всех затрат на хранение от начала процесса до произвольного момента t можно определить по формуле:
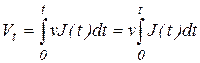
За общий интервал времени работы Θ данная формула приобретает вид:
Т.е. суммарная стоимость затрат на хранение пропорциональна интегралу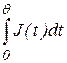 
. Т.к. геометрический смысл интеграла состоит в том, что его значение равно площади фигуры, заключенной между осью абсцисс и графиком функции на интервале [0, Θ], то в тех случаях, когда площадь легко вычислить, определение величины затрат на хранение запасов упрощается.
Date: 2015-09-20; view: 1952; Нарушение авторских прав