Краткая теория. Интерференция с помощью бипризмы Френеля

Интерференция с помощью бипризмы Френеля.

При наложении когерентных волн интенсивность 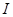результирующей волны в каждой точке пространства определяется выражением: 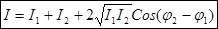(1), где 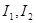- интенсивности накладывающихся волн, 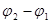- разность фаз возбуждаемых волнами колебаний.

Интенсивность, наблюдаемая при наложении не когерентных волн равна сумме интенсивностей, создаваемых каждой из волн в отдельности: 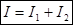(2). В случае когерентных волн 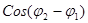имеет постоянное значение во времени, но свое для каждой точки пространства. В тех точках пространства, для которых 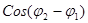>0, 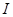будет превышать 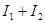, в точках, для которых 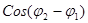<0, 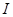будет меньше 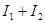. Таким образом, при наложении когерентных волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн. Особенно отчетливо проявляется интерференция в том случае, когда интенсивность обеих интерферирующих волн одинакова: 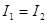. Тогда в минимумах 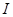=0, в максимумах 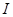=. Для некогерентных волн при том условии появляется всюду одинаковая освещенность 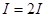. Член 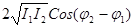в формуле (1) называется интерференционным числом. Рассмотрим две когерентные монохроматические световые волны (рис.1), исходящие из действительных или мнимых источников 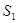и 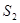, имеющих вид параллельных светящихся тонких нитей или щелей. Область OPQ, в которой эти волны перекрываются, называются полем интерференции. Во всей этой области наблюдается чередование мест с максимальной и минимальной интенсивностью. Если в поле интерференции внести экран Е, то на нем будет видна интерференционная картина, которая в случае цилиндрических волн имеет вид чередующихся светлых и темных полос. Вычислим ширину этих полос в предположении, что экран параллелен плоскости, проходящей через источник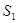и и 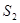. Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении перпендикулярном к линиям 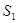и 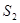(рис.2). Начало отсчета выберем в точке 0, относительно которо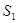й и 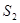расположены симметрично. Источники будем называть колеблющимися в одинаковой фазе. Из рис.2 следует, что 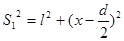; 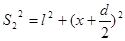из этого следует, что 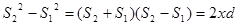. Для получения различимо интерференционной картины, расстояние между источниками d должно быть значительно меньше расстояния до экрана l. Расстояние х, в пределах которого образуются интерференционные полосы должно быть значительно меньше l. При этих условиях можно положить . В среде с показателем преломления n=1, разность 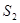- 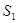дает оптическую разность хода: 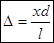(3). Максимумы интенсивности будут наблюдаться при значениях х, равных: 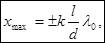k=0,1,2…(4), минимумы при х, равных 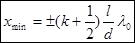, k=0,1,2…(5). Расстояние 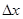между двумя соседними минимумами называют шириной интерференционной картины. Ширина полосы очевидно равна: 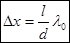(6). Ширина интерференционных полос и расстояние между ними зависят от длины волны 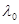. Только в центре картины, при 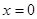совпадут максимумы всех длин волн. По мере удаления от центра картины максимумы разных цветов смещаются все больше и больше. Это приводит к смазыванию интерференционных полос, при наблюдении их в белом свете. В монохроматическом свете число различных полос в интерференции возрастает. Измерив, расстояние между полосами 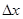и зная l и d по формуле (6) можно вычислить длину волны света: 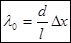(7).

Одним из методов получения интерференционной картины является использование бипризмы Френеля, которая представляет изготовленную из одного куска стекла две призмы с малым преломляющим углом 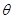~28'. Призмы имеют общее основание.

Определим число интерференционных полос, наблюдаемых при использовании бипризмы Френеля. Пусть источник света S располагается на расстоянии a от бипризмы (рис.3). Угол падения на бипризму мал, вследствие чего все лучи отклоняются бипризмой на одинаковый угол 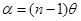, где 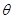- преломляющий угол призм. В результате образуются два когерентные цилиндрические волны, исходящие из мнимых источников 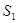и 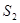, лежащих в одной плоскости с S. Расстояние между источниками равно: 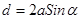~ 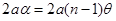. Здесь 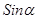может быть заменен углом в силу малости угла 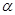. Расстояние от источников до экрана равно: 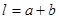. Ширину интерференционной полосы находим из уравнения (6): 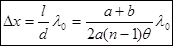(8).

Область перекрытия волн (поле интерференции PQ) имеет протяженность: 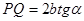~ 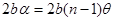. Отсюда число наблюдаемых полос равно: 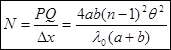(9).

Date: 2015-09-05; view: 806; Нарушение авторских прав