
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение истинного и магнитного азимутов и дирекционного угла направления по карте
|
|
Для определения по карте истинного азимута направления через начальную его точку В, используя минутную разграфку градусной рамки, проводят истинный меридиан, относительно которого геодезическим транспортиром измеряют величину истинного азимута А (рис. 24). Зная величины склонения магнитной стрелки о и сближения меридианов у, можно рассчитать магнитный азимут и дирекционный угол данного направления, исходя из формул (4) и (5):
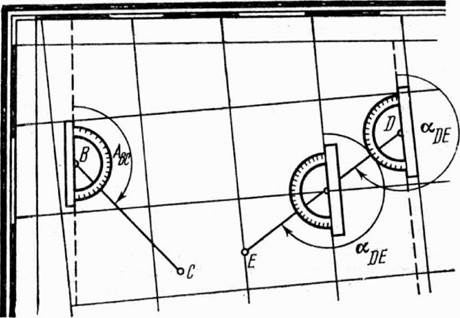 Рис. 60 Схема определения истинного азимута и дирекционного угла направления на карте.
Ам = А - о; а = А - у.
Для определения по карте дирекционного угла направления ОЕ через начальную его точку В проводят линию, параллельную оси абсцисс, т. е. вертикальной линии километровой сетки, и относительно ее измеряют транспортиром дирекционный угол аОЕ (см. рис. 24). Дирекционный угол заданной линии можно замерить в любой точке ее пересечения с вертикальной линией километровой сетки.
Если известны (либо определены графически) координаты хъ уг и х2,у2, начальной и конечной
точек линии, то дирекционный угол данного направления может быть рассчитан по формуле
Рис. 60 Схема определения истинного азимута и дирекционного угла направления на карте.
Ам = А - о; а = А - у.
Для определения по карте дирекционного угла направления ОЕ через начальную его точку В проводят линию, параллельную оси абсцисс, т. е. вертикальной линии километровой сетки, и относительно ее измеряют транспортиром дирекционный угол аОЕ (см. рис. 24). Дирекционный угол заданной линии можно замерить в любой точке ее пересечения с вертикальной линией километровой сетки.
Если известны (либо определены графически) координаты хъ уг и х2,у2, начальной и конечной
точек линии, то дирекционный угол данного направления может быть рассчитан по формуле
|
^ = ^.
Х2 Х1
На практике для решения указанных задач обычно сначала находят дирекционный угол направления, а затем, зная склонение магнитной стрелки о и сближение меридианов у, переходят к истинному и магнитному азимутам, исходя из формул (5) и (6):
А = а + у; Ам = а - а + у = а — П.
Средние значения о и у для данного листа карты приводятся на схеме и в пояснениях в юго- западном углу карты.
§ 37. РЕШЕНИЕ ЗАДА Ч ПО ПЛАНУ ИЛИ КАРТЕ С ГОРИЗОНТАЛЯМИ
Определение высот точек по горизонталям. Отметка точки, расположенной на горизонтали, равна отметке этой горизонтали. Если горизонталь не оцифрована, то ее отметка находится по оцифровке соседних горизонталей с учетом высоты сечения рельефа.
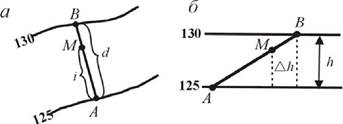
Более общим является случай, когда точка находится между двумя горизонталями. Пусть точка М (рис. 25, а), отметку которой требуется определить, расположена между горизонталями с отметками 125 и 130 м.
Через точку М проводят прямую АВ как кратчайшее расстояние между горизонталями и на плане измеряют заложение й = АВ и отрезок I = АМ. Как видно из вертикального разреза по линии АВ (рис. 25,6), величина ЛЬ представляет собой превышение точки М над младшей горизонталью. Из подобия треугольников АВВ' и АММ' следует:
|
АИ _ _/_ И ё
 М' В'
Рис. 61. Схема определения отметок точек по горизонталям:
а,б - точка расположена между разноименными горизонталями; в - точка расположена между одноименными горизонталями Отсюда
М' В'
Рис. 61. Схема определения отметок точек по горизонталям:
а,б - точка расположена между разноименными горизонталями; в - точка расположена между одноименными горизонталями Отсюда
|
АИ _-И. ё
Тогда
Нм = НА + Ак = НА + - к.
ё
Для приведенного на рис. 25, а примера
| 14 20 |
| '5 т = 128,5 т. |
Нм = 125 т +
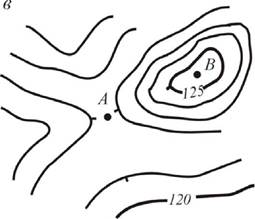
Если точка расположена между горизонталями с одинаковыми отметками (точка А на рис. 25, в) либо внутри замкнутой горизонтали (точка В), то ее отметку можно определить лишь приближенно. При этом считают, что отметка точки меньше или больше высоты этой горизонтали на половину высоты сечения рельефа, т. е. 0,5Ь (например, НА= 121,5м, Нв= 125,5м). Поэтому отметки характерных точек рельефа (вершина холма, дно котловины и т. п.), полученные из измерений на местности, выписывают на планах и картах.
Определение крутизны скатов и уклонов линий по горизонталям, Графики заложений. Крутизна ската (угол наклона ската) V и уклон линий г между точками, лежащими на соседних горизонталях, определяются по известной формуле:
И
г _ д _-.
ё
отсюда
И
V _ агс!д—, ё
где И - высота сечения рельефа, м; ё - заложение, м.
Чтобы избежать расчетов при определении уклонов и крутизны скатов по плану или карте, на практике пользуются специальными графиками, называемыми графиками заложений.
Для построения графика заложений горизонтальную линию делят на равные отрезки произвольной длины и у концов отрезков подписывают значения углов наклона, начиная с 30'. Предельное значение углов на шкале графика назначают в зависимости от максимальной крутизны скатов данного плана или карты. Затем вычисляют заложения, соответствующие каждому значению угла наклона при принятой высоте сечения рельефа, по формуле
ё _ И.
№
Полученные величины заложений, выраженные в масштабе плана (карты), откладывают на перпендикулярах к горизонтальной линии против соответствующих углов наклона. Через полученные точки проводят плавную линию и получают график заложений, называемый в данном случае графиком крутизны (рис. 26,а).
Если у точек деления горизонтальной линии вместо углов наклона подписаны значения углов и на перпендикулярах отложены соответствующие заложения, то получают график уклонов (рис. 26,6).
Для определения крутизны ската или уклона с плана берут в раствор циркуля соответствующее заложение (например, АВ), переносят его на график заложений (см. рис. 26) так, чтобы отрезок АВ оказался параллельным линиям графика, а одна ножка циркуля располагалась на горизонтальной линии, другая - на кривой. Значение крутизны или уклона определяют, пользуясь оцифровкой горизонтальной шкалы графика.
В рассматриваемом примере (см. рис. 26) крутизна ската V=1о30', а уклон /=0,026.
Необходимо помнить, что графики заложений, приводимые за оформительской рамкой, рассчитываются и строятся соответственно сечению рельефа и масштабу данного плана или карты.
Проектирование трассы с заданным уклоном. При проектировании железных и шоссейных дорог, каналов и других протяженных объектов возникает необходимость наметить на карте (плане) трассу будущего сооружения с заданным уклоном.
Пусть на плане масштаба 1: 10000 требуется наметить трассу шоссейной дороги между точками М и N чтобы уклон ее во всех частях не превышал /=0,05 (рис. 27). Высота сечения рельефа на плане И = 5 м.
Для решения задачи рассчитывают заложение, соответствующее заданному уклону г и высоте сечения рельефа И,
| = 100т |
5т
ё _ И _
г 0,05т
и выражают его в масштабе плана:
,, ё, т -100 100т -100, ё _- _ _ 1ст,
М
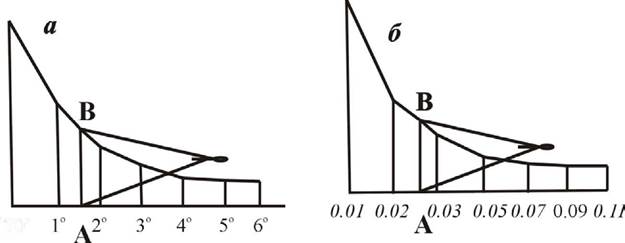 Рис.62. Графики заложений:а - крутизны; б - уклонов
Рис.62. Графики заложений:а - крутизны; б - уклонов
|
| 0°30' |
где М - знаменатель численного масштаба плана.
Величину заложения й' можно определить также по графику заложений.
Раствором циркуля, равным заложению ё= 1 см, из точки М засекают соседнюю горизонталь и получают точку 1; из точки 1 тем же раствором засекают следующую горизонталь, получая точку 2, и т. д. Соединив полученные точки, проводят линию с заданным уклоном.
 Рис. 63.Схема проектирования трассы с заданным уклоном.
Если рассчитанное заложение ё' окажется меньше расстояния между двумя соседними горизонталями (т. е. уклон ската на данном участке меньше заданного), то участок трассы проводится по кратчайшему расстоянию между ними. При проектировании дорог последнее расценивается как положительный фактор.
Следует отметить, что решение данной задачи позволяет наметить несколько вариантов трассы, из которых выбирается наиболее приемлемый по технико-экономическим соображениям.
Рис. 63.Схема проектирования трассы с заданным уклоном.
Если рассчитанное заложение ё' окажется меньше расстояния между двумя соседними горизонталями (т. е. уклон ската на данном участке меньше заданного), то участок трассы проводится по кратчайшему расстоянию между ними. При проектировании дорог последнее расценивается как положительный фактор.
Следует отметить, что решение данной задачи позволяет наметить несколько вариантов трассы, из которых выбирается наиболее приемлемый по технико-экономическим соображениям.
|
Построение профиля местности по заданному направлению. При
проектировании инженерных сооружений, а также для определения видимости между точками местности необходимо построение профиля местности по заданному направлению.
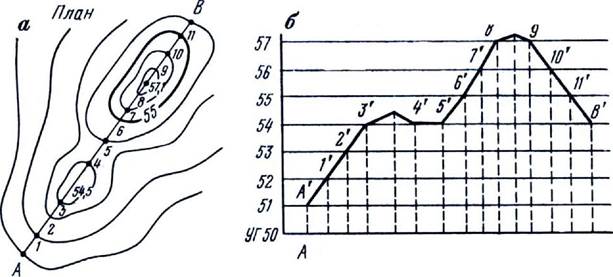
Для построения профиля по линии АВ (рис. 28, а) на листе бумаги проводят горизонтальную линию и на ней в масштабе плана последовательно откладывают отрезки А - 1, 1 - 2; 2 - 3, 3 - отм. 54,5 и т. д.
Выбирают условный горизонт таким образом, чтобы его линия не пересекалась с линией профиля (например, УГ = 50 м). В каждой из полученных точек восставляют перпендикуляры (рис. 28, б) и на них в принятом вертикальном масштабе откладывают профильные отметки, равные разности абсолютных отметок точек и условного горизонта, т. е. Нпроф=Набс—УГ. Соединив полученные точки А', 1, 2' и т. д. плавной кривой, получают профиль местности по линии АВ. Для большей наглядности вертикальный масштаб профиля обычно принимается в 10 раз крупнее горизонтального масштаба, т. е. масштаба плана.
Определение границы водосборной площади. Водосборной площадью или бассейном называется участок земной поверхности, с которой вода по условиям рельефа должна стекать в данный водосток (реку, лощину и т. д.). Оконтуривание водосборной площади производится с учетом рельефа местности по горизонталям карты (плана).
Границами водосборной площади служат линии водоразделов, пересекающие горизонтали под прямым углом. На рис. 29 линии водоразделов показаны пунктиром.
Профиль по А-6
 / 2 3 Щ5Ч 5 6 7 8Ц19 Ю П В
Рис.64.Профиль местности по заданному направлению
/ 2 3 Щ5Ч 5 6 7 8Ц19 Ю П В
Рис.64.Профиль местности по заданному направлению
|
Зная водосборную площадь, среднегодовое количество осадков, условия испарения и впитывания влаги почвой, можно подсчитать мощность водного потока, которая необходима для расчета мостов, площадок дамб и других гидротехнических сооружений.
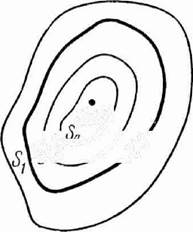
Определение объемов земляных тел. Используя план с горизонталями, можно вычислить объемы земляных тел, представляющих собой холмы или горы, либо объемы пространств, образуемых впадиной или котловиной.
Объем пород, заключенных в холме (рис. 30), может быть представлен как сумма объектов, заключенных между соседними горизонталями. Объем каждого пояса определится по приближенной формуле объема усеченного конуса: для I пояса
= И 1 2
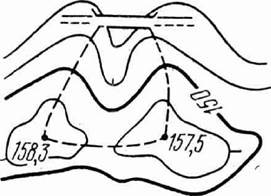 Рис.65.Схема определения границы водосборной площади.
Рис.65.Схема определения границы водосборной площади.
|
|
| щ ^гУФ |
| Рис.66.Схема определения объемов земляных тел. |
для II пояса
= + и 2
И т.д.
где к - высота сечения рельефа; 8;, 81+1 - площади нижнего и верхнего оснований пояса, ограниченные горизонталями; в зависимости от необходимой точности определяются графически либо с помощью планиметра.
Если верхний слой холма имеет форму купола, то его объем определится по приближенной формуле
ув = >2 8вк,
где 8В - площадь основания верхнего слоя; к' - разность отметок горизонтали основания верхнего слоя и вершины холма. Тогда общий объем холма
г=1
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ ПО ПЛАНУ ИЛИ КАРТЕ
Для решения многих инженерных задач требуется знать площади участков местности. Эти площади могут быть измерены по плану или карте графическим, аналитическим и механическим способами либо их комбинациями. Следует иметь в виду, что по планам (картам) площадь определяется с меньшей точностью, чем по результатам непосредственных измерений на местности; при этом на точность определения площадей, кроме погрешностей измерений на местности, оказывают влияние погрешности построения плана (карты) и измерений на них, а также деформация бумаги.
Графический способ определения площадей. Для определения площадей небольших участков по плану или карте применяется графический способ с разбивкой участка на геометрические фигуры либо с помощью палеток.
|
. /
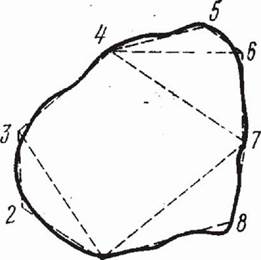
Рис.67. Способ определения площади с разбивкой участка на геометрические фигуры
В первом случае искомую площадь небольшого (до 10—15 см2 в плане) участка разбивают на простейшие геометрические фигуры: треугольники, прямоугольники, трапеции (рис. 31). При криволинейном контуре участка его разбивка на геометрические фигуры выполняется с таким расчетом, чтобы стороны фигур по возможности ближе совпадали с этим контуром. Затем на плане (карте) измеряют соответствующие элементы фигур (длины оснований и высоты) и по геометрическим формулам вычисляют площади этих фигур. Площадь всего участка определяется как сумма площадей отдельных фигур.
Точность определения площади в рассматриваемом случае во многом зависит от масштаба плана (карты): чем мельче масштаб, тем грубее измеряется площадь. Поскольку графическая погрешность линейных измерений на плане (1гр=0,2 мм) не зависит от длины отрезков, то относительная погрешность короткой линии будет больше, чем длинной. Поэтому заданный участок следует разбивать на фигуры возможно больших размеров с примерно одинаковыми длинами оснований и высот.
Для контроля и повышения точности площадь участка определяется дважды, для чего строят новые геометрические фигуры или в треугольниках измеряют другие основания и высоты. Относительное расхождение в результатах двукратных определений общей площади участка не должно превышать 1:200.
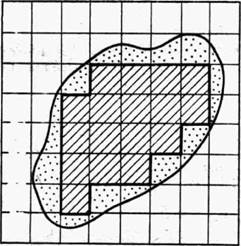
Определение площадей (до 2-3 см2) участков с резко выраженными криволинейными границами рекомендуется производить с помощью квадратной палетки. Палетка представляет собой (рис. 32, а) лист прозрачной основы (стекла, целлулоида или восковки), на которую нанесена сетка квадратов со сторонами 1- 5 мм. Зная длину сторон и масштаб плана, легко вычислить площадь квадрата палетки з.
Для определения площади участка палетку произвольно накладывают на план и подсчитывают число N полных квадратов, расположенных внутри контура участка. Затем оценивают на глаз число квадратов N2, составляемых из неполных квадратов у границ участка. Тогда общая площадь измеряемого участка
Рис.68.. Способы определения площадей с помощью палеток: а - квадратной, б - линейной, в - курвиметр.
5 = #1 +
Для контроля площадь заданного участка измеряют повторно, развернув палетку примерно на 45°. Относительная погрешность определения площади палеткой составляет 1:50—1:100.
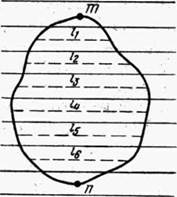
При определении площадей до 10 см2 можно использовать параллельную (линейную) палетку (рис. 32, б), представляющую собой лист прозрачной основы, на которой через равные промежутки а =2—5 мм нанесен ряд параллельных линий.
Палетка накладывается на заданный участок таким образом, чтобы крайние точки т и П контура разместились посредине между параллельными линиями палетки. В результате измеряемая площадь оказывается расчлененной на фигуры, близкие к трапециям с равными высотами; при этом отрезки параллельных линий внутри контура являются средними линиями трапеции. Следовательно, для определения площади участка с помощью циркуля-измерителя и масштабной линейки нужно измерить длины средних линий трапеций II, 12,...1„ и их сумму умножить на расстояние между линиями с учетом масштаба плана, т. е.
п
5 = а(I, + 1г +... + 1п) = а^ 1п.
г =1

|
|
|
Суммарная длина отрезков может быть замерена с помощью курвиметра (рис. 32, в) - прибора для измерения длин линий на плане (карте). Для этого колесо курвиметра последовательно прокатывают по измеряемым линиям и по разности начального и конечного отсчетов на циферблате определяют суммарную длину отрезков в сантиметрах плана. Для контроля измеряют площадь при втором положении палетки, развернув ее на 60—90° относительно первоначального положения.
|
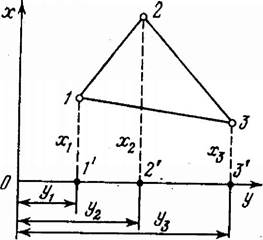
Рис.69. Аналитический способ определения площади.
Аналитический способ определения площадей. Если по результатам измерений на плане (карте) определены координаты вершин замкнутого многоугольника, то площадь последнего может быть определена аналитическим способом.
Пусть известны прямоугольные координаты вершин треугольника /—2—3 (рис. 33). Опустив из его вершин перпендикуляры на ось Оу, площадь треугольника можно представить как алгебраическую сумму площадей трех трапеций: I - (1 —1—2—2'), II - (2'—2—3—3') и III - (1/ - 1 - 3 - 3), т. е.
8 =81+8Ц+8Ш.
Площади рассматриваемых трапеций определяются так:
81 = У (Х1 + Х2) (У2 - У1); 811 = У (Х1 + Х2) (У2 - У1); 8ш = У (Х1 + Х2) (У2 - У1).
Тогда удвоенная искомая площадь треугольника 1—2—3 будет равна:
28 = (Х 1 + Х 2) (У 2- У 1) + (Х 2 + Х з) (У з- У 2)- (X I + Х з) (Уз — У 1)-
После раскрытия скобок, соответствующей группировки членов уравнения и вынесения за скобки общих знаменателей получим
28 =Х1 (У 2- У з) + Х 2 (У з- У2) + Хз (У 1— У 2)-
или
28 =у1 (Х з- Х 2) + У 2 (Х 1- Х3) + Уз (Х 2 —Х 1)-
В общем виде
1 -з
8 = 2 2 х- ((+1- Ум)
г=1
или
1 '=з
8 = ^2 У г ((+1 - Хм)
г =1
Тогда для многоугольника с числом вершин п при их оцифровке по ходу часовой стрелки формулы общего вида запишутся так:
1 -з
8 = 2 2 х (+1- Ум)
г=1 1 г=3
8 =Т2 У г ((+1 - Ъ-Л
21=1
где 1=7, 2, 3,...., п.
Для контроля вычисления производят по обеим формулам. Если координаты точек получены по результатам измерений на местности, то точность способа повышается, так как при этом на точность вычисления площади влияют лишь погрешности угловых и линейных измерений на
местности. Так, при измерении углов с точностью 1' и длин линий с точностью 1:2000 относительная погрешность определения площади составит примерно 1: 500.
При определении площадей сложной конфигурации с большим числом вершин вычисления рекомендуется проводить с использованием ЭВМ.
Date: 2015-09-19; view: 1775; Нарушение авторских прав