
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Б) покупается после выпуска и погашается в конце срока;
|
|
В) покупается и продается в пределах объявленного срока.
Для варианта а получим знакомое равенство (10.7):
л i +
Д, дч
*'эп| = />2-
Однако символы здесь имеют другое содержание, а именно: Рх — номинал, Р2 — цена при продаже (определяется рыночной ставкой процента), д,, д2 — сроки до погашения.
Доходность владения сертификатом в течение д{ — д2 дней определяется формулой (10.8), если расчет исходит из цен сертификата. Если же в качестве исходных параметров берутся процентные ставки #, и /2 (/, — объявленная ставка сертификата, /2 — ставка рынка в момент продажи), то
I.
-1
d, -d2
(10.12)
В случае когда измерителем эффективности выступает сложная процентная ставка и заданы цены, получим формулу, аналогичную (10.10). Наконец, если расчет основан на уровнях процентных ставок, то
U + *2'*2 J
(10.13)
Отметим, что доходность операции имеет место только в том случае, когда d{i{>d2i2. Предельное значение ставки /', при котором инвестор получит доход, равно
/, <
в|/
Перейдем теперь к варианту б. Здесь справедливо равенство
| ' = л(1 +4ы |
| -^ |
л-1 I = Р 11 +
AI +
где Рх — номинал, Р2 — цена приобретения, / — объявленная процентная ставка.
| Время |
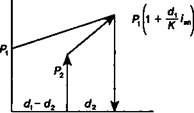 Контур операции для данного уравнения приведен на рис. 10.3. s
Контур операции для данного уравнения приведен на рис. 10.3. s
Рис. 10.3
Из приведенного выше равенства получим значение /эп при заданной величине Р2:
1 д\ •! + -£'■
-1
(10.14)
Если в качестве измерителя эффективности принята ставка сложных процентов, то
| ЛИ + 4/ |
Л.
К
-1.
(10.15)
Рассмотрим вариант в. Здесь покупка производится спустя некоторое время после выпуска сертификата, а его продажа — до момента погашения. В этом случае опять приходим к уравнению (10.7), в котором Р{ означает цену приобретения (а не номинал). Отсюда для расчета /эп и /э пригодны формулы (10.8M10.il).

 ПРИМЕР 10.5. Операция заключается в покупке сертификата за 1020 тыс. руб. за 160 дней до его выкупа. Инструмент был продан за 1060 тыс. руб. через 90 дней. Какова доходность операции, измеренная в виде простой и сложной ставок? Исходные данные Р, = 1020, Р2 = 1060, д^ = 160, д2 = 70, д1 - д2 = 90.
ПРИМЕР 10.5. Операция заключается в покупке сертификата за 1020 тыс. руб. за 160 дней до его выкупа. Инструмент был продан за 1060 тыс. руб. через 90 дней. Какова доходность операции, измеренная в виде простой и сложной ставок? Исходные данные Р, = 1020, Р2 = 1060, д^ = 160, д2 = 70, д1 - д2 = 90.
Пусть временная база простых процентов равна 365 дням, тогда по формуле (10.8) находим
1060 - 1020 365
х -тт~ = 0,159, или 15,9%.
Эквивалентная сложная ставка равна
1 +
90 365
Х 0,159
365/90
- 1 =0,169, или 16,9%.
Величину /э можно определить и непосредственно по формуле (10.10):
'э =
365/90
- 1 =0,169.
ПРИМЕР 10.6. Финансовый инструмент, приносящий постоянный процент, куплен за 200 дней до срока его погашения и продан через 100 дней. В момент покупки процентная ставка на рынке была равна 10%, в момент продажи — 9,8%. Доходность операции купли-продажи в виде годовой ставки сложных процентов равна согласно (10.13)
_ 365 + 200x0,1 ^365/ioo 'э " I 365 + 100 х 0,098
- 1 =0,103, или 10,3%.
ПРИМЕР 10.7. Сертификат с номиналом 100 тыс. руб. с объявленной доходностью 12% годовых (простые проценты) сроком 720 дней куплен за 110 тыс. руб. за 240 дней до его оплаты. Какова доходность инвестиций в виде /э?
Если К = 360 дней, то по формуле (10.15) получим
100-
720 1 +—~-х0,12 360
365/240
- 1 =0,19985, или 19,985%.
Date: 2015-09-19; view: 428; Нарушение авторских прав