Камеральные работы при теодолитной съемке

Прямая геодезическая задача. Как уже указывалось, в геодезии принята си­стема плоских прямоугольных координат, в которой относительно оси Х Х, совпадающей с направлением меридиана, и оси УУ, перпен­дикулярной к оси ХХ, определяют положение каждой точки, т. е. ее координаты Х и У; при этом счет четвертей идет по ходу часовой стрелки, согласно возрастанию азимутов и дирекционных углов (на рис. четверти показаны римскими цифрами).

При составлении планов ситуацию наносят от опорных точек и линий, их соединяющих. Поэтому на бумагу сначала наносят опор­ные точки по их координатам, которые вычисляют в первую очередь, решая прямую геодезическую задачу. Она состоит в том, что по из­вестным координатам данной точки, а также по дирекционному углу и горизонтальному проложению линии от этой точки до опре­деляемой вычисляют координаты определяемой точки. Например, известны координаты точки А (x_а, y_а), горизонтальное проложение d линии АВ, дирекционный угол α линии АВ/

На рис. видно, что x_b = x _а + ВВ₁; y_b = y _а + АВ₁. От­резки ВВ₁ и АВ₁, представляющие собой проекции линии АВ на оси координат, или разность координат точек В и А, называют приращениями координат и обозначают ∆x и ∆y. Поэтому можно написать:

x _b =x _a +∆x,

y _b =y _a +∆y,

∆x и ∆y из прямоугольного треугольника АВВ₁ равны:

∆x = d cos α,

∆y= d sin α.

Тогда координаты точки В будут:

x _b =x _a + d cos α,

y _b =y _a + d sin α,

Данные формулы остаются справедливыми для вычисления прира­щений координат по румбам сторон, т. е

∆x = d cosr,

∆y= d sinr.

Знаки приращений координат зависят только от направления линии, т. е. от названия румба.

Для северных направлений (СВ, СЗ) ∆x имеет знак плюс, для южных направлений (ЮВ, ЮЗ) - знак минус. Для восточных направлений (СВ, ЮВ) ∆y имеет знак плюс, а для западных направ­лений (СЗ, ЮЗ) - знак минус.

Для вычисления координат точек хода предварительно проводят уравнивание результатов полевых измерений.

^ Уравнивание углов поворота сомкнутого теодолитного хода. Из геометрии известно, что теоретическая сумма углов многоугольника

∑β_t=180º(n-2),

где п - число углов хода.Однако практически измерение углов теодолитом сопровождается рядом ошибок, что приводит к некоторому отклонению суммы измеренных углов ∑β_п от теоретической; это отклонение носит название угловой невязки f_β и вычисляется так:

f_β= ∑β_п-∑β_t

Эта невязка не должна превышать предельную величину, которую определяют по формуле:

∆β=±1′√n.

Необходимо, чтобы f_β ≤ ∆β.

В том случае, когда полученная угловая, невязка допустима, т. е. меньше или равна предельной, в углы вводят поправки. Можно считать, что все углы измеряют с одинаковой точностью, поэтому угловую невязку нужно разделить на число измеренных углов и полученную поправку внести в каждый угол поровну с обратным зна­ком невязки. При таком распределении каждый исправленный угол будет иметь дробные значения минут, что создает неудобство при дальнейших вычислениях. Обычно угловую невязку распределяют проще: в первую очередь вводят поправки в углы с дробными долями минут так, чтобы округлить их до половины минуты. Оставшуюся часть невязки распределяют по пол минуте на углы, ограниченные более короткими сторонами, так как в этом случае из всех перечислен­ных ошибок особенно скажется влияние неточного центрирования прибора и установки вехи над точкой наведения.

^ Вычисление дирекционных углов сторон теодолитного хода. После уравнивания измеренных углов приступают к вычислению дирекционных углов сторон теодолитного хода. В замкну­том теодолитном ходе ABCDE (рис. 67, а) правые углы хода β₁, β₂,…β₅ исправлены.

Если через каждую из вершин хода ABCDE провести прямые, параллельные осевому меридиану, тогда α_l, α₂,... будут дирек­ционные углы, которые требуется вычислить для решения прямой задачи. Дирекционный угол одной из сторон, например АВ, должен быть известен. Если он равен α₁, то, продолжив прямую АВ, полу­чим:

α₂=α₁+180º-β₂,

α₃=α₂+180º-β_3, и т. д.

В общем виде:

α_n=α_n-1+180º-β_n

^ Вычисление, уравнивание приращений координат и вычисление координат пунктов теодолитного хода.

Сумма приращений координат в замкнутом ходе теоретически должна быть равна нулю. Практически же вследствие неизбежных ошибок при измерении, особенно линий, в этих приращениях появятся невязки. Для замкнутого хода невязки будут равны:

f_x= ∑∆x_п

f_y= ∑∆y_п,

где f_x и f_y – невязки в приращениях координат.

По невязкам приращений координат находят абсолютную линейную невязку:

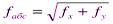
В точности выполненных работ убеждаются по относительной линейной невязке:

f_отн= f_абс/L,

где L – периметр хода.

Относительную невязку выражают простой дробью с единицей в числителе. В теодолитных ходах 1 разряда относительная невязка недолжна превышать 1:2000 и входах 2 разряда 1:1000.

Если невязка допустима, вычисленные приращения исправляют. Невязки f_x и f_y распределяют так, чтобы поправки в приращениях были пропорциональны длине сторон со знаком, противоположным знаку невязки.

Найденные поправки алгебраически суммируют с соответствующими приращениями и получают исправленные приращения координат, сумма которых должна быть равна теоретической. По исправленным приращениям координат от точек с известными координатами последовательно вычисляют координаты всех точек хода.

^ Составление плана по результатам теодолитной съемки.

Планы вычерчивают на хорошей чертежной бумаге, раз­мер листа зависит от размера участка и выбранного масштаба плана. При построении плана по координатам опорных точек в первую оче­редь строят координатную сетку. Для этого применяют специальную линейку Дробышева. Это металлическая линейка с шестью вырезами посередине. Один из краев каждого выреза скошен: у первого вы­реза, помеченного нулем, - по прямой линии, у всех остальных по дугам окружностей с радиусами 10,20, 30, 40, 50 см от начального штриха. Конец линейки скошен по дуге радиуса 70,711 см. Этой линейкой можно построить координатную сетку на площади ква­драта со стороной 50 см, а также на площади прямоугольника со сторонами (катетами) 30, 40 см и диагональю 50 см

Для построения сетки квадратов линейку кладут параллельно нижнему краю листа бумаги и, отступив от него на 5-7 см, проводят по скошенному краю линейки тонкую линию. Затем линейку сдви­гают и по скошенному краю каждого выреза пересекают прочерченную линию штрихами.

Укладывают линейку вдоль левого края листа совмещают нулевой штрих с точкой А - пересечением прямой с крайним левым штрихом; следят, чтобы ось линейки была примерно

перпендикулярна к прямой АВ. Проводят штрихи по каждому скошенному вырезу.

Кладут линейку по диагонали, совместив нулевой штрих с крайним правым штрихом в точке В. По концу линейки про­черчивают дугу, пересекающую последний верхний штрих в точке С. Таким образом построен прямоугольный треугольник АВС со сто­ронами 50; 50; 70,711 см

Точно так же строят второй треугольник, для чего укладывают линейку, г) сначала по линии BD, а затем по диагонали AD и получают второй треугольник ABD. Проверяют верхнюю сто­рону CD, отклонение может быть допущено не более 0,2 мм. На стороне CD по прорезям линейки отмечают 10-сантиметровые от­резки. Полученные противоположные штрихи соединяют тонкими линиями. Координатная сетка должна быть построена очень точно, так как ошибки в сетке сказываются на точности построения плана. Для контроля построения сетки циркулем-измерителем проверяют равенство диагоналей всех квадратов.

Построение плана. Если координаты вычисляют от условного начала Х = О, У = О и значения этих координат невелики, то одну из вертикальных линий сетки принимают за ось Х, а одну из гори­зонтальных - за ось У. В их пересечении х = 0, y = 0. Намечая начало координат, учитывают размер плана и назначают начальными такие линии сетки, при которых точки с самыми малыми и самыми большими значениями координат разместятся в пределах сетки координат, а план – в центре листа.

Если координаты вычислены в общегосударственной зональной системе, левой крайней линии придают значение ординаты, близкое к наименьшему значению ординаты точки хода, а нижней горизонтальной линии придают абсциссу, близкую к наименьшей абсциссе хода.

Затем относительно известных линий и точек, руководствуясь абрисом, наносят на план подробности, снятые на местности. Способы нанесения контурных точек те же, какие были применены для их съемки на местноти. Однако действия совершают при этом в обратном порядке.

Date: 2015-09-19; view: 1490; Нарушение авторских прав