Детальная разбивка круговых кривых

Детальная разбивка переходных и круговых кривых выполняется в период строительства после выноса на трассу трех основных точек кривой НК, СК, КК. Детальная разбивка производится через 5 м при радиусах кривых менее 100 м, через 10 м при радиусах кривых менее 500 м и через 20 м – более 500 м. Для детальной разбивки кривых наиболее часто используется способ прямоугольных координат (рис. 3).

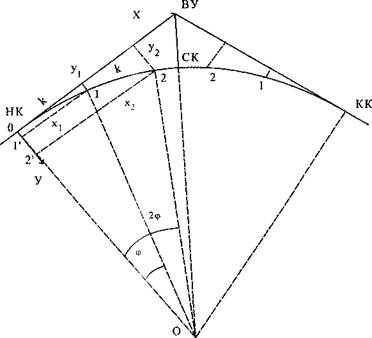
Рис. 3 Способ прямоугольных координат

За начало координат принимают точку НК – начала круговой кривой, ось X располагают по тангенсу кривой в направлении ВУ, ось У направлена по радиусу к центру круговой кривой О.

Выбирают интервал разбивки К и для этого значения рассчитывают угол φ = (К/R)ρ, по которому определяют значения прямоугольных координат х и у для детальной разбивки.

х₁= R×sin φ, х₂= R×sin 2φ, х₃=R×sin 3φ,..., х_n= R×sin nφ;

(4)

у₁= R×sin²(φ/2), y₂=sin²φ, y₃=R×sin²(3φ/2), …, y_n=R×sin²(nφ/2)

Вдоль тангенсов (ось абсцисс) откладывают длины х, восстанавливают прямой угол в полученной точке. Точка 1 круговой кривой фиксируется расстоянием у, отмеренным по перпендикуляру. Так же и получают другие точки круговой кривой. Вторую половину круговой кривой разбивают от ее конца, выполняя аналогичные действия и используя значения х и у, по­лученные для первой половины. Как видно из геометрии способа, для его реализации требуется свободное пространство. Достоинство способа прямоугольных координат состоит в том, что каждая точка кривой выносится независимо от других с примерно одинаковой точностью.

Если участок трассы расположен в закрытой местности, то удобнее использовать способ продолженных хорд (рис. 4).

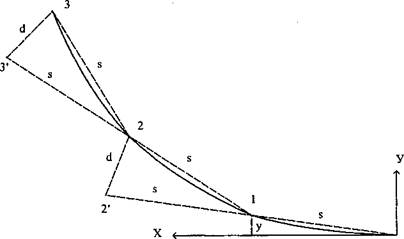
Рис. 4 Способ продолженных хорд

В этом способе первая точка выносится по способу прямоугольных координат. Затем хорда продолжается на ее же длину s, и получается вспомогательная точка 2'. На базе 12' при помощи линейной засечки расстояниями s и d =s2/R получается точка 2 круговой кривой. Вновь продолжают хорду, но уже от точки 2. вдоль отрезка 21. Из точек 23' повторяют линейную засечку отрезками s и d, получая точку 3 и т.д.

В некоторых случаях при трассировании объектов возникает необходимость выноса пикета на круговую кривую.

Вынос осуществляется методом прямоугольных координат (рис. 5)

Вначале вычисляется значение К – интервала круговой кривой между пикетом и началом круговой кривой.

К = ПК n – ПК _НК

Зная К можно получить угол φ

К = R×φ/ρ, а φ = К×ρ/R

Используя значение φ получим координаты x и y

х= R×sin nφ; у = R×sin²(φ/2) (5)

Date: 2015-09-19; view: 3816; Нарушение авторских прав