Проложение тахеометрического хода

1.Вычислим сумму измеренных горизонтальных левых углов разомкнутого тахеометрического хода β^Σ _изм:

β^Σ _изм =β₂₅ +β₁+β₂+β₃+β₄+β₂₇;

2.Определим теоретическую сумму горизонтальных углов тахеометрического хода β^Σ _теор по формуле ():

β^Σ _теор =α_к-α_н+180° n, ()

где α_к, α_н- дирекционные углы начальной и конечной твердых сторон; n- число углов в разомкнутом ходе;

3.Вычислим фактическую угловую невязку ƒ_β по формуле ():

ƒ_β= β^Σ _изм - β^Σ _теор ()

4.Определим величину допустимой угловой невязки ƒ_{β доп}

по формуле():

ƒ_{β доп} =2 t , ()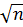

где t =0,5';

ƒ_{β доп} =2·0,5' 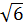=2,0';

в нашем случае вычисленная угловая невязка ƒ_β превышает допустимую невязку, поэтому дальнейший расчет не будет отвечать заданным требованиям точности.

5.Распределим фактическую невязку ƒ_β в виде поправок ν _i, где i =1, n, в измеренные значения горизонтальных углов с таким расчетом, чтобы их сумма равнялась невязке с обратным знаком, причем большие поправки будем вводить в углы с наименьшими сторонами;

β₂₅ ^испр =β₂₅+ν₁

β₁ ^испр = β₁ +ν₂

β₂ ^испр =β₂ + ν₃

β₃ ^испр =β₃+ν₄

β₄ ^испр = β₄ +ν₅

β₂₇ ^испр = β₂₇ +ν₆

произведем контроль уравнения по тождеству ():

β₂₅ ^испр + β₁ ^испр + β₂ ^испр + β₃ ^испр +β₄ ^испр +β₂₇ ^испр = β^Σ _теор; ()

следовательно, расчет выполнен правильно.

6.Рассчитаем дирекционные углы α и соответствующие им румбы r сторон тахеометрического хода по исправленным значениям его горизонтальных левых углов по формуле ():

α _{i +1}=α _i + β ^испр_i -180°, ()

где α _{i +1,} α _i –дирекционные углы последующего и текущего направлений;

β ^испр_i – исправленный горизонтальный левый угол, образованный последующим и текущим направлениями хода;

α _н – угол четвертой четверти, следовательно,

r_н =360°- α _н;

α_25-1=α _н + β ^испр ₂₅- 180°;

α_25-1 – угол четвертой четверти, следовательно,

r _25-1=360° - α_25-1;

α_1-2 = α_25-1+ β₁ ^испр - 180°;

α_1-2 – угол четвертой четверти, следовательно,

r _1-2 = 360°- α_1-2;

α_2-3= α_1-2+ β₂ ^испр - 180°;

α_2-3 - угол четвертой четверти, следовательно,

r _2-3 = 360°- α_2-3;

α_3-4= α_2-3+ β₃ ^испр - 180°;

α_3-4 – угол третьей четверти, следовательно,

r _3-4 = α_3-4 - 180°;

α_4-27= α_3-4+ β₄ ^испр - 180°;

α_4-27 – угол четвертой четверти, следовательно,

r _4-27 = 360°- α_4-27;

α_{К =} α_4-27+β₂₇^{[ испр ]} - 180^o;

что соответствует известном углу α_к конечной твердой стороны - значит расчет выполнен правильно;

α_к^{[ испр ]} – угол первой четверти, следовательно,

r _к = α_к^{[ испр ]};

7. Выполним расчет приращений координат Δ x _i и Δ y _i по формулам (6) и (7) и определим их суммы (Δ x ^[Σ] _{выч ,} Δ y ^[Σ] _выч ):

Δ x _i = S _i cos r _i,

Δ y _i = S _i sin r _i ,

Где S _i – горизонтальное проложение i -ной линии хода;

| Δ x _25-1|= S _25-1 cos r _25-1

| Δ y _25-1|= S _25-1 sin r _25-1

так как α_25-1 – угол четвертой четверти, то

Δ x _25-1 = +

Δ y _25-1 = –

| Δ x _1-2|= S _1-2 cos r _1-2

| Δ y _1-2|= S _1-2 sin r _1-2

так как α_1-2 – угол четвертой четверти, то

Δ x _1-2 = +

Δ y _1-2 = –

| Δ x _2-3|= S _2-3 cos r _2-3

| Δ y _2-3|= S _2-3 sin r _2-3

так как α_2-3 – угол четвертой четверти, то

Δ x _2-3 = +

Δ y _2-3 = –

| Δ x _3-4|= S _3-4 cos r _3-4

| Δ y _3-4|= S _3-4 sin r _3-4

так как α_3-4 – угол четвертой четверти, то

Δ x _3-4 = –

Δ y _3-4 = –

| Δ x _4-27|= S _4-27 cos r _4-27

| Δ y _4-27|= S _4-27 sin r _4-27

так как α_3-4 – угол четвертой четверти, то

Δ x _4-27 = +

Δ y _4-27= –

Δ x ^[Σ]_выч, = Δ x _25-1 + Δ x _1-2 + Δ x _2-3 + Δ x _3-4 + Δ x _4-27 ;

Δ y ^[Σ]_выч = Δ y _25-1 + Δ y _1-2 + Δ y _2-3 + Δ y _3-4 + Δ y _4-27;

8. Определим теоретическую сумму приращений Δ x ^[Σ] _теор и Δ y ^[Σ] _теор по формулам (8) и (9):

Δ x ^[Σ] _теор = x_k – x_н , (8)

Δ y ^[Σ] _теор = y_к –y_н , (9)

где = x_k, x_н , y_к, y_н - абсциссы и ординаты соответственно известных конечной и начальной твердых точек хода;

Δ x ^[Σ] _теор = x₂₇ – x ₂₅

Δ y ^[Σ] _теор = y ₂₇ –y₂₅

9. Определим линейные невязки в приращениях координат ƒ _x и ƒ _y по формулам (10) и (11):

ƒ _x = Δ x ^[Σ]_выч, – Δ x ^[Σ] _теор, (10)

ƒ _y = Δ y ^[Σ]_выч – Δ x ^[Σ] _теор (11)

10. Вычислим абсолютную линейную невязку по формуле (12):

ƒ _s = ƒ _x² + ƒ _y²; (12)

11. Вычислим относительную линейную невязку по формуле (13) и сравним ее с допустимой:

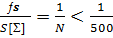(13)

где S ^[Σ] - периметр полигона;

N – округленное целое число;

S ^[Σ] = S _25-1 + S _1-2 + S _2-3 + S _3-4 + S _4-27 ;

следовательно, дальнейший расчет будет отвечать заданным требования точности.