
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Медиана и мода
|
|
Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние.
Структурные средние - вспомогательные характеристики изучаемой совокупности. Мода и медиана считаются типичными характеристиками только однородной совокупности с большим количеством единиц.
Мода (Мо) - числовое значение признака, которое наиболее часто встречается у единиц совокупности. Мода для интервальных рядов определяется по формуле:
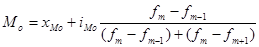 ,
,
где: xМо - нижняя граница модального интервала;
iМо - величина модального интервала;m - частота модального интервала;m-1 - частота интервала, предшествующего модальному;m+1 - частота интервала, следующего за модальным.
На основе данных табл. 1 рассчитаем моду для размера грузооборота:
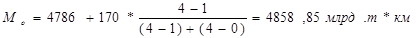
Таким образом, у наибольшего количества лет данной совокупности размер грузооборота составляет 4858,85 млрд. т*км.
Медиана - это величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Для интервального ряда распределения медиана рассчитывается по формуле:
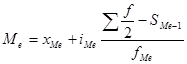 ,
,
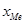 - верхняя граница предмедианного интервала
- верхняя граница предмедианного интервала
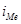 - величина медианного интервала
- величина медианного интервала
 - полусумма накопленных частот
- полусумма накопленных частот
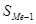 - сумма частот, накопленных до начала медианного интервала
- сумма частот, накопленных до начала медианного интервала
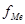 - число наблюдений в медианном интервале.
- число наблюдений в медианном интервале.
На основе данных табл.1 построим вспомогательную таблицу, по которой рассчитаем медиану для интервального ряда:
Таблица 3. Вспомогательная таблица для расчета медианы
| № | Размер грузооборота, млрд.т*км | количество лет | Сумма накопленных частот |
| 4446-4616 | |||
| 4616-4786 | |||
| 4786-4948 |
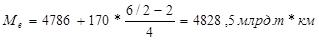
Следовательно, при размере грузооборота в 4828,5 млрд. т*км вся совокупность разделяется на две равные части.
Date: 2015-09-18; view: 715; Нарушение авторских прав