
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ЗАДАЧА № 1
|
|
Студент 4 курса Преподаватель
Мыльников Е. А. А.В.
Шифр: 0813 - п/АТС-1034
МОСКВА 20012 г.
ЗАДАЧА № 1
По стальному проводу (электрическая проводимость 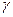 = 107(Ом
= 107(Ом 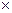 м)-1; относительная магнитная проницаемость
м)-1; относительная магнитная проницаемость 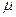 =103 ) диаметром 2
=103 ) диаметром 2 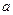 =6,04 мм течет синусоидальный ток
=6,04 мм течет синусоидальный ток 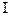 =100А частотой
=100А частотой 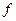 Гц
Гц
Определить плотность тока на поверхности и на оси провода.
Вариант численного значения частоты тока определяется по формуле:
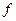 = 1,38866 п2 Гц,
= 1,38866 п2 Гц, 

где п - последняя цифра шифра студента (цифра О соответствует п = 10).
Привести вывод формул для определения плотности тока  и напряженности
и напряженности 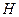 в любой точке сечения провода, не учитывая влияния обратного провода на поле в прямом проводе. При решении задачи использовать цилиндрическую систему координат.
в любой точке сечения провода, не учитывая влияния обратного провода на поле в прямом проводе. При решении задачи использовать цилиндрическую систему координат.
Решение задачи следует начать с обязательной проверки соотношения между током проводимости и током смещения в данном проводнике, что является важным обоснованием для всех последующих рассуждений.
Решение:
1. Приведем вывод формул для определения плотности тока  и напряженности
и напряженности 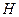 в любой точке сечения провода, не учитывая влияния обратного провода на поле в прямом проводе.
в любой точке сечения провода, не учитывая влияния обратного провода на поле в прямом проводе.
Для этого рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью 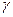 и магнитной проницаемостью
и магнитной проницаемостью 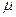 а. Первое и второе уравнения Максвелла, записанные в комплексной форме для синусоидально изменяющихся во времени
а. Первое и второе уравнения Максвелла, записанные в комплексной форме для синусоидально изменяющихся во времени 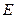 и
и 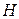 имеют вид:
имеют вид:
1) 
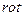
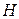 =
= 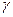
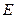 +
+ 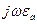
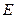
2) 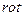
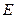 = -
= - 
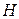
Так как в проводящей среде даже при очень высоких частотах произведение 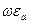 намного меньше проводимости
намного меньше проводимости 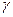 . Следовательно, произведением
. Следовательно, произведением 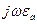
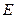 в первом уравнении Максвелла для проводящих сред можно пренебречь.
в первом уравнении Максвелла для проводящих сред можно пренебречь.
Вектор плотности тока  , записанный в комплексной форме для синусоидально изменяющихся во времени
, записанный в комплексной форме для синусоидально изменяющихся во времени  и тока I, удобно направить в положительном направлении оси Z, поэтому
и тока I, удобно направить в положительном направлении оси Z, поэтому  =Z0
=Z0  .
.
Таким образом первое и второе уравнения Максвелла для проводящей среды приобретают вид:
1) 
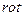
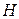 =
= 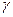
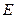 =
= 
2) 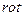
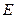 = -
= - 
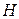
Умножив второе уравнение Максвелла на проводимость 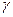 , получим:
, получим:
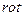
 = -
= - 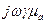
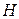
Возьмем ротор от последнего уравнения:
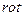
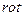
 = grad div
= grad div  -
- 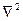
 =-
=- 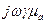
 ,
,
или, считая процесс течения тока установившимся, т.е. div  = 0, и подставляя
= 0, и подставляя  =Z0
=Z0  , перейдем к скалярному уравнению:
, перейдем к скалярному уравнению:
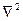
 =
= 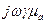

Данное уравнение решим в цилиндрической системе координат. Учитывая, что в данной системе координат вид оператора 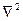 = div grad, а также то, что
= div grad, а также то, что  от
от 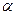 и от z не зависит (из соображений симметрии), получим:
и от z не зависит (из соображений симметрии), получим:
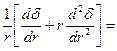
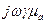

или 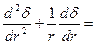
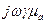
 .
.
Введем обозначение q2 = - 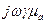 ,тогда уравнение примет вид:
,тогда уравнение примет вид:
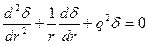
или 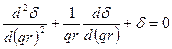
Последнее уравнение является частным случаем уравнения Бесселя относительно аргумента х = qr и функции у =  . Его решение имеет вид:
. Его решение имеет вид:
 = AJ0 (qr) + BN0 (qr),
= AJ0 (qr) + BN0 (qr),
где А и В - постоянные интегрирования;
J0 (qr) - функция Бесселя нулевого порядка первого рода;
N0 (qr) - функция Бесселя нулевого порядка второго рода.
Функция Бесселя нулевого порядка второго рода обращается в бесконечность на оси провода, т.е. при r = 0. Но так как плотность тока должна быть всюду конечна, в том числе и на оси провода, то примем В = 0. Следовательно, решение имеет вид:
 = AJ0 (qr)
= AJ0 (qr)
Используя второе уравнение Максвелла, определим напряженность магнитного поля:
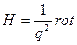

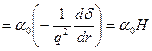
Отсюда
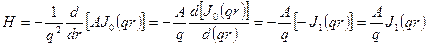 ,
,
где J1 (qr) - функция Бесселя первого рода первого порядка.
Определим постоянную интегрирования А, для чего полученное выражение для Н, взятое на поверхности провода (при r = а) приравняем к известному выражению для Н из закона полного тока:
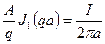 ,
,
откуда 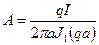
Подставим найденное значение А в полученные выше выражения для  и Н:
и Н:
 =
= 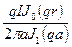
Н= 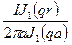
С помощью этих формул можно определить комплекс плотности тока  и комплекс напряженности поля Н в любой точке сечения провода. Радиус r может принимать значения от 0 до а. Для точек на оси провода r = 0; для точек на поверхности провода r = а.
и комплекс напряженности поля Н в любой точке сечения провода. Радиус r может принимать значения от 0 до а. Для точек на оси провода r = 0; для точек на поверхности провода r = а.
Так как Jo (0) = 1, то плотность тока на оси провода:
 0=
0= 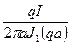
Подставим данное выражение в формулу решения:  =
=  0 J0 (qr). Тогда плотность тока на поверхности провода:
0 J0 (qr). Тогда плотность тока на поверхности провода:  a=
a=  0 J0 (qa). Очевидно, что произведение (qr) есть комплексное число:
0 J0 (qa). Очевидно, что произведение (qr) есть комплексное число:
qr = r 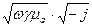
Бесселевы функции от комплексного аргумента также являются комплексными и могут быть представлены в показательной форме:
J0 (qr) = 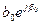
J1 (qr) = 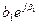 ,
,
где 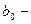 модуль;
модуль;
 аргумент функции J0 (qr);
аргумент функции J0 (qr);
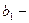 модуль;
модуль;
 аргумент функции J1 (qr), которые определяются по значению r
аргумент функции J1 (qr), которые определяются по значению r  с помощью таблицы 1.
с помощью таблицы 1.
Таблица 1
Таблица модулей и аргументов функций J0 (qr) и J1 (qr)
r 
| 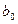
| 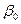 , rpад. , rpад.
| 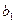
| 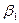 , rpaд. , rpaд.
|
| О | О | О | - 45,00 | |
| 1,015 | 14,22 | 0,501 | - 37,84 | |
| 1,229 | 52,28 | 1,041 | - 16,73 | |
| 1,95 | 96,52 | 1,80 | 15,71 | |
| 3,439 | 138,19 | 3,173 | 53,90 | |
| 6,231 | 178,93 | 5,812 | 93,55 | |
| 11,501 | 219,62 | 10,850 | 133,45 | |
| 21,548 | 260,29 | 20,50 | 173,51 | |
| 40,82 | 300,92 | 39,07 | 213,69 | |
| 77,96 | 341,52 | 74,97 | 253,95 | |
| 149,8 | 382,10 | 144,58 | 294,27 |
В данной таблице учтено наличие множителя 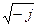 в составе аргумента (qr).
в составе аргумента (qr).
2. Проверим соотношение между током проводимости в стале и током смещения в данном проводнике.
Пусть: 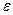 = 10;
= 10; 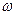 = 100 рад / с. Тогда отношение:
= 100 рад / с. Тогда отношение:
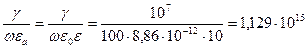 ,
,
где электрическая постоянная 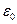 = 8,86. 10-12 Ф/м.
= 8,86. 10-12 Ф/м.
Из данного соотношения можно сделать вывод, что увеличение частоты 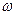 даже на несколько порядков не существенно повлияет на изменение соотношения между током проводимости в стали и током смещения в данном проводнике. Следовательно, ток проводимости в проводнике во много раз больше тока смещения.
даже на несколько порядков не существенно повлияет на изменение соотношения между током проводимости в стали и током смещения в данном проводнике. Следовательно, ток проводимости в проводнике во много раз больше тока смещения.
3. Определим частоту переменного тока f.
f= 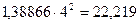 Гц.
Гц.
4. Рассчитаем параметр 
так как 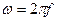 , то
, то  =
= 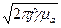 ,
,
где 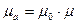 ;
;  Гн/м
Гн/м
Следовательно,  =
= 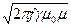
 =
= 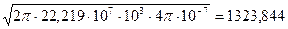 м –1
м –1 
5. Определим комплексную величину q
q= 1323,844 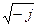 =1323,844
=1323,844 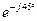
6. Выражение a  =
= 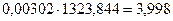
7. По таблице 1 найдем:
J0 (qa) = J0 (3,998 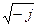 )=
)= 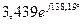 ; b0 = 3,439;
; b0 = 3,439; 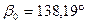 .
. 
J1 (qa) = J1 (3,998 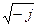 )=
)=  ; b1 = 3,173;
; b1 = 3,173; 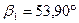 .
.
J0 (0) = 1  ; b0 = 1;
; b0 = 1; 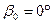 .
.
J1 (0) = 0 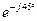 ; b1 = 0;
; b1 = 0; 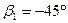 .
.
8. Определим плотность тока на оси провода:
 0=
0= 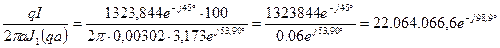 А/м2.
А/м2.
9. Определим плотность тока на поверхности провода:
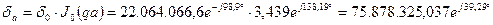 А/м2.
А/м2.
Date: 2015-09-18; view: 781; Нарушение авторских прав