
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Транспортные задачи энергетики. Транспортная матрица. Распределительный метод. Метод потенциалов. Учет пропускной способности линий. Транспортная задача с транзитом мощности
|
|
Цель занятия:
- изучить понятие транспортной задачи;
- изучить способы решения транспортных задач.
Практическое задание:
Пример 3.1. В системе электроснабжения имеется два узла с источниками питания и три узла потребителей. Составить математическую модель для решения транспортной задачи и найти допустимое решение транспортной задачи. Взаимное расположение узлов показано на рис. 3.1.
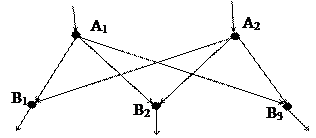 |
Рис. 3.1. Расположение узлов питания и потребления
Исходные данные:
· А1 =50, А2 =30 – мощности источников питания;
· В1 =20, В2 =25, В3 =35 – мощности потребителей, ед.м.;
· сkp – удельные затраты на передачу мощностей по линиям между узлами источников и потребителей, у.е./ед.м.
Математическая модель:
Особенности транспортной задачи следующие:
- все ограничения имеют форму равенств;
- все коэффициенты при переменных в системе ограничений равны плюс единице;
- каждая переменная дважды входит в систему ограничений;
- один раз в балансы узлов источников, второй раз в балансы узлов
потребителей.
Необходимо найти такое распределение мощностей от источников к приемникам, при котором затраты на передачу мощностей будут минимальными.
Целевая функция:
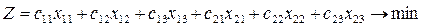
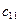 =1,2,
=1,2, 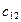 =1,8,
=1,8, 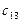 =1,5,
=1,5, 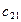 =1,6,
=1,6, 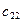 =2,3,
=2,3, 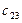 =2,1.
=2,1.
Ограничения, представляющие собой балансы мощности в узлах электрической сети, будут иметь вид:
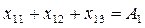
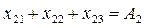

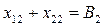
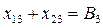
Граничные условия:
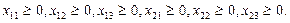
Получение допустимого решения:
Запишем решение в табличной форме – транспортной матрицей.
Таблица 3.1
 =20
с11 =1,2 =20
с11 =1,2
| 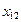 =0 =0
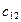 =1,8 =1,8
| 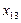 =30 =30
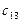 =1,5 =1,5
| 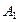 =50 (50-20=30) =50 (50-20=30)
|
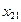 =0 =0
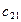 =1,6 =1,6
| 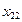 =25 =25
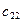 =2,3 =2,3
| 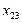 =5 =5
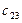 =2,1 =2,1
|  =30 =30
|
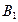 =20 =20
| 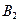 =25 =25
|  =35 (35-30=5) =35 (35-30=5)
| 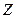 =137 =137
|
Выберем клетку с минимальным значением сkp (с11 =1,2). Занесем в качестве базисной переменной х11 меньшее из А1 и В1 (В1 =20). Баланс для 1-го столбца соблюден, в остальные клетки столбца заносим 0.
Выберем клетку с минимальным значением сkp (с13 =1,5). Занесем в качестве базисной переменной х13 меньшее из А1 и В3 (А1 =30). Для баланса 3-го столбца занесем во вторую клетку 5.
Для баланса 1-ой строки занесем во вторую клетку 0. Для баланса 2-ой строки во вторую клетку занесем
Итак, вся транспортная матрица заполнена. Балансы мощности по строкам (по узлам источников) и по столбцам (по узлам потребителей) выполняются. Все переменные неотрицательны. Полученное исходное решение является допустимым. В этом решении
свободные переменные: х12 =0, х21 =0;
базисные переменные: х11 =20, х13 =30, х22 =25, х23 =5 е.м.;
значение целевой функции
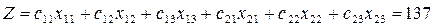
Пример 3.2. Решить предыдущую задачу распределительным методом.
В полученном допустимом решении имеются две свободные переменные х12 и х21. Произвольно выберем переменную х21 и увеличим значение этой переменной от нуля до единицы х21 =1.
Таблица 3.3
 =19
с11 =1,2 =19
с11 =1,2
| 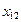 =0 =0
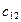 =1,8 =1,8
| 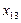 =31 =31
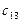 =1,5 =1,5
| 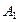 =50 (50-19=31) =50 (50-19=31)
|
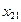 =1 =1
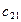 =1,6 =1,6
| 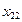 =25 =25
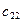 =2,3 =2,3
| 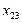 =4 =4
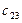 =2,1 =2,1
|  =30 =30
|
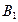 =20 =20
| 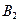 =25 =25
|  =35 =35
| 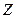 =136,8 =136,8
|
Видно, что при увеличении свободной переменной х21 значение целевой функции уменьшается. Эту свободную переменную следует перевести в базис.
Таблица 3.4
 =15
с11 =1,2 =15
с11 =1,2
| 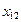 =0 =0
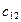 =1,8 =1,8
| 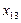 =35 =35
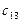 =1,5 =1,5
| 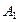 =50 =50
|
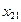 =5 =5
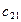 =1,6 =1,6
| 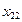 =25 =25
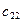 =2,3 =2,3
| 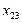 =0 =0
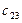 =2,1 =2,1
|  =30 =30
|
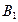 =20 =20
| 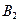 =25 =25
|  =35 =35
| 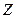 =136 =136
|
Видно, что значение целевой функции улучшилось по сравнению с предыдущим решением (136<137).
Пример 3.3. Решить предыдущую задачу методом потенциалов.
В соответствии с методом потенциалов каждой строке и каждому столбцу транспортной матрицы присваивается свой потенциал: строкам - потенциалы Vi (i =1, 2,... n), столбцам - потенциалы Uj (j =1, 2,... m), как показано в табл. 3.5 для рассматриваемого примера.
Таблица 3.5
| U1 =1 | U2 =1,7 | U3 =1,3 | ||
| V1 =0,2 |  =15
с11 =1,2 =15
с11 =1,2
| 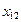 =0 =0
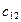 =1,8 =1,8
| 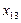 =35 =35
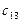 =1,5 =1,5
| 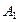 =50 =50
|
| V1 =0,6 | 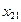 =5 =5
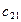 =1,6 =1,6
| 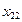 =25 =25
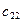 =2,3 =2,3
| 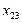 =0 =0
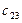 =2,1 =2,1
|  =30 =30
|
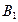 =20 =20
| 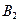 =25 =25
|  =35 =35
| 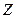 =136 =136
|
Эти потенциалы таковы, что для каждой базисной переменной сумма потенциалов равна удельной стоимости.
U1 =1;
V1= с11 - U1 = 1,2 - 1 = 0,2;
V2= с21 - U1 = 1,6 - 1 = 0,6;
U2= с22 - V2 = 2,3 - 0,6 =1,7;
U3= z13 - V1 = 1,5 - 0,2 = 1,3.
В общем случае, при условии
Vi +Uj > zij
перевод свободной переменной xij в базис уменьшает целевую функцию Z, а при условии
Vi +Uj < zij
перевод свободной переменной хij в базис увеличивает целевую функцию Z.
Для свободной переменной х23
V2+U3 = 0,6+1,3=1,9 < z23 =2,1.
Для свободной переменной х12
V1+U2 = 0,2+1,7=1,9 > z12 =1,8.
Следовательно, свободную переменную х12 следует перевести в базис, поскольку этот перевод приведет к уменьшению целевой функции Z.
Новому допустимому решению соответствует транспортная матрица табл. 3.6.
Таблица 3.6
| U1 =1 | U2 =1,7 | U3 =1,4 | ||
| V1 =0,1 |  =0
с11 =1,2 =0
с11 =1,2
| 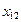 =15 =15
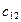 =1,8 =1,8
| 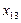 =35 =35
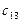 =1,5 =1,5
| 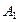 =50 =50
|
| V1 =0,6 | 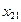 =20 =20
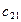 =1,6 =1,6
| 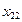 =10 =10
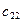 =2,3 =2,3
| 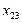 =0 =0
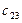 =2,1 =2,1
|  =30 =30
|
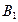 =20 =20
| 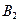 =25 =25
|  =35 =35
| 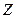 =134,5 =134,5
|
Полученное решение является оптимальным.
Пример 3.4. Решить задачу рассмотренного выше примера для случая, когда мощность, передаваемая по линии х13, ограничена величиной 20 е.м. (х13 < 20)
В исходной транспортной матрице (табл. 3.2) третий столбец разбиваем на два столбца с условными потребителями В 3'=35-20=15 и В 3"=20 е.м. Удельную стоимость передачи мощности от источника А 1 к условному потребителю В 3' примем равной 100 у.е./е.м. Остальные удельные стоимости такие же.
Таблица 3.7
| U1 =1 | U2 =1,6 | U’3 =1,4 | U”3 =1,3 | ||
| V1 =0,2 |  =20
с11 =1,2 =20
с11 =1,2
| 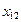 =10 =10
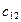 =1,8 =1,8
| 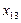 =0 =0
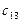 =100 =100
| 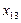 =20 =20
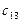 =1,5 =1,5
| 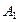 =50 =50
|
| V1 =0,7 | 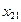 =0 =0
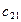 =1,6 =1,6
| 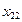 =15 =15
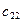 =2,3 =2,3
| 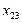 =15 =15
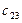 =2,1 =2,1
| 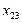 =0 =0
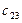 =2,1 =2,1
|  =30 =30
|
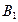 =20 =20
| 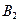 =25 =25
| 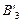 =15 =15
| 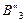 =20 =20
| 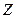 =138 =138
|
Далее используем метод потенциалов.
Пример 3.5. В проектируемой системе электроснабжения имеется 2 узла источников питания и 2 узла потребителей. Мощности источников составляют A 1=100 и A 2=50, а мощности потребителей - B 3=90 и B 4=60 е.м. Удельные затраты на передачу мощностей по линиям между узлами составляют z 12=10, z 13=5, z 14=2, z 23=4, z 24=3 и z 34=2 у.е./е.м.
Требуется найти оптимальную схему электрической сети
Составим транспортную матрицу.
Таблица 3.8
| U1 =1 | U2 =2 | U3 =6 | U4 =3 | ||
| V1 =0,2 | A1 =100 | ||||
| V2 =-2 | A2 =50 | ||||
| V3 =-6 | B3 =0 | ||||
| V4 =-3 | B4 =0 | ||||
| A1 =0 | A2 =0 | B3 =90 | B4 =60 | Z=520 |
Справа от матрицы, где помещены мощности источников питания, указаны нулевые мощности узлов 3 и 4 (В 3=0, В 4=0), поскольку эти узлы не являются источниками. Снизу под матрицей, где помещены мощности потребителей, указаны нулевые мощности узлов 1 и 2 (А 1=0, А 2=0), поскольку эти узлы не являются потребителями.
Исходное допустимое решение найдено методом наименьшей удельной стоимости.
Зададимся произвольно значением одного из потенциалов (U 1=1). Вычисленные значения остальных потенциалов показаны в табл. 3.8. Поскольку для базисных транзитных переменных удельные стоимости zii =0, потенциалы с одинаковыми индексами равны по величине и противоположны по знаку Vi = - Ui.
Далее используем метод потенциалов.
Таблица 3.8
| U1 =1 | U2 =1 | U3 =5 | U4 =3 | ||
| V1 =-1 | A1 =100 | ||||
| V2 =-1 | A2 =50 | ||||
| V3 =-5 | B3 =0 | ||||
| V4 =-3 | -40 | B4 =0 | |||
| A1 =0 | A2 =0 | B3 =90 | B4 =60 | Z=480 |
Практическое занятие 4
Нелинейные оптимизационные задачи. Градиентный метод. Метод неопределенных множителей Лагранжа. Задача оптимального распределения активной мощности в энергосистеме. Задача оптимального распределения компенсирующих устройств.
Цель занятия:
- изучить понятие нелинейной оптимизационной задачи;
- изучить способы решения нелинейных оптимизационных задач.
Практическое задание:
Пример 4.1. В существующей схеме электроснабжения (рис. 4.1) требуется определить мощности компенсирующих устройств Qк1 и Qк2 в узлах 1 и 2 исходя из условия минимума суммарных затрат на установку этих устройств и покрытие потерь активной мощности в схеме.
Исходные данные:
напряжение схемы U = 10 кВ;
сопротивления линий R1 =6 Ом, R2 =4 Ом;
реактивные нагрузки узлов 1 и 2 Q1 =600 квар и Q2 =800 квар;
удельные затраты на установку компенсирующих устройств z0 =0,5 у.е./квар;
удельные затраты на покрытие потерь активной мощности с0 =10 у.е./кВт.
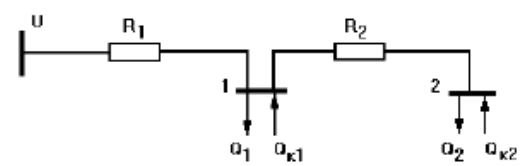
Рис. 4.1. Схема электроснабжения
Целевая функция, представляющая собой суммарные затраты на установку компенсирующих устройств и покрытие потерь активной мощности в схеме, имеет следующий вид
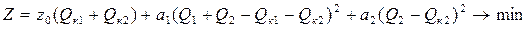
где 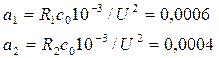
Для решения задачи выберем метод покоординатного "спуска". Определим частные производные целевой функции Z по переменным Qk1 и Qk2:
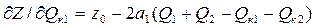
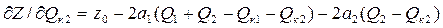
Примем исходное приближение: Qk1 0=0 Qk2 0=0.
 у.е.;
у.е.;
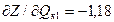 ;
;
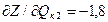 .
.
Очевидно, что в направлении переменной Qk2 целевая функция Z убывает сильнее, чем в направлении переменной Qk1.
Начнем спуск в направлении переменной Qk2.
Примем величину шага λ=400 квар. Первое приближение (первый шаг) будет Qk11 =0, Qk21 =400 квар. Значение целевой функции Z1 =864 у.е.
Второй шаг: Qk1 2=0, Qk22 =800 квар. Значение целевой функции Z2 = 616 у.е.
Третий шаг: Qk13 =0, Qk23 =1200 квар. Значение целевой функции Z3 = 689 у.е.
Очевидно, что "спуск" по координате Qk2 целесообразно прекратить, поскольку Z3>Z2, и вернуться к значениям переменных Qk12 =0, Qk22 =800 квар, полученным на втором шаге.
Выполним новый третий шаг λ=400 квар в направлении другой переменной Qk1: Qk13 =400 квар, Qk23 =800 квар. Значение целевой функции Z3 = 624 у.е. Движение в направлении переменной Qk1 нецелесообразно, поскольку Z3>Z2.
Точка с координатами Qk1 =0, Qk2 =800 квар находится в окрестности минимума целевой функции Z. При принятой длине шага λ=400 квар более точное решение получено быть не может.
Пример 4.2. В существующей схеме электроснабжения (рис. 4.2) следует распределить между узлами 1, 2 и 3 суммарную мощность компенсирующих устройств, равную 1000 квар. Критерий оптимальности - минимум потерь активной мощности.
Исходные данные:
напряжение схемы U =10 кВ;
сопротивления линий R1 =0,4, R2 =0,5, R3 =0,6 Ом;
реактивные нагрузки узлов Q1 =600, Q2 =500, Q3 =400 квар.

Рис. 4.2. Схема электроснабжения
В соответствии с исходными данными подлежащие минимизации потери активной мощности (целевая функция) определяются соотношением.
∆Р= a1 (Q1+Q2+Q3-Qk1-Qk2-Qk3) 2+ a2(Q2 - Qk2) 2+a3(Q3-Qk3)2 =
= 0,004(1500 -Qk1-Qk2-Qk3) 2+ 0,005(500 -Qk2) 2+ 0,006(400 -Qk3) 2 → min,
где a1= R1 /U2 =0,004;
a2= R2 /U2 =0,005.
a3= R3 /U2 =0,006.
Суммарная мощность источников реактивной мощности ограничивается условием
Qk1 + Qk2 + Qk3 - 1000=0.
В соответствии с выражением (4.16) функция Лагранжа будет иметь вид
L = 0,004(1500 - Qk1 - Qk2 - Qk3)2 + 0,005(500 - Qk2)2 +
+0,006(400 - Qk3)2+λ(Qk1 + Qk2 - Qk3 - 1000)2 → min.
Для определения минимума функции Лагранжа вычислим ее частные производные по всем переменным и приравняем эти производные к нулю:
∂L/∂Qk1 = - 0,008(1500 - Qk1 - Qk2 - Qk3)+ λ =0,
∂L/∂Qk2 = - 0,008(1500 - Qk1 - Qk2 - Qk3)- 0,01(500 - Qk2) + λ=0,
∂L/∂Qk3 = - 0,008(1500 - Qk1 - Qk2 - Qk3) - 0,012(400 - Qk3)+ λ=0,
∂L/∂λ = Qk1+ Qk2+ Qk3 - 1000 = 0.
Откуда Qk1 = 100 квар; Qk2 = 500 квар; Qk3 = 400 квар;
λ = 0,008(1500 - 100 - 500 - 400)= 4.
∆Р= 2 кВт.
Практическое занятие 5
Date: 2015-09-18; view: 2388; Нарушение авторских прав