Математическая модель оптимизационной задачи в энергетике. Методы решения оптимизационных задач. Анализ решения оптимизационной задачи

Цель занятия:

- изучить основные понятия и определения;

- научиться составлять математические модели оптимизационных задач энергетики;

- изучить методы решения оптимизационных задач.

Практическое задание:

Дать определение следующим понятиям:

Критерий оптимальности

Детерминированная информация

Случайная информация

Недетерминированная информация

Целевая функция

Ограничения

Граничные условия

Непрерывная переменная

Целочисленная переменная

Дискретная переменная

Пример 1. Определить максимальную прибыль предприятия выпускающего продукцию трех видов (i = 1, 2, 3). Для каждого изделия i -го вида требуются три типа ресурсов: энергетические, финансовые и сырьевые.

Исходные данные:

- наличие на предприятии каждого j -го ресурса b_j;

- норма расхода j -го ресурса на одно изделие i -го вида a_ji;

- прибыль z_i от реализации одного i -го изделия;

- минимальное количество b₄ всех видов изделий, которое предприятие должно выпустить.

Решение.

Обозначим искомые количества 1-го, 2-го и 3-го видов изделий через х₁, х₂ и х₃.

Поскольку необходимо найти максимальную прибыль предприятия, этот экономический критерий и выразим целевой функцией. Прибыль от реализации изделий i -го вида есть произведение z_ix_i. Подлежащая максимизации суммарная прибыль от реализации трех видов изделий (целевая функция) будет иметь следующий вид:

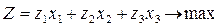
Перейдем к составлению ограничений. Поскольку на одно изделие 1-го вида требуется а₁₁ единиц энергии, на искомое количество х₁ потребуется а₁₁х₁ единиц энергии. Для искомых количеств изделий 2-го и 3-го видов потребуется соответственно а₁₂х₂ и а₁₃х₃ единиц энергии. Суммарный расход энергии на выпуск трех видов изделий составит а₁₁х₁ + а₁₂х₂ + а₁₃х₃ единиц энергии. Эта величина ограничена наличием на предприятии энергетических ресурсов в количестве b₁. Таким образом, ограничение по энергетическим ресурсам будет иметь вид

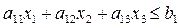
Аналогично составляются ограничения по финансовым и сырьевым ресурсам.

Ограничение минимального суммарного количества выпускаемых изделий запишется как

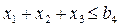
В итоге, вся система ограничений будет иметь вид

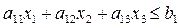
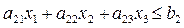
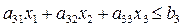
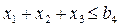
При этом 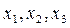принимают целые неотрицательные значения.

Представленные выше выражения являются математической моделью оптимизационной задачи. Рассматриваемая оптимизационная задача относится к классу линейных задач, решение которой возможно методами линейного программирования.

Практическое занятие 2

Date: 2015-09-18; view: 502; Нарушение авторских прав