Материальной точки

Введем в рассмотрение радиус-вектор 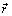, определяющий положение материальной точки в инерциальной системе отсчета, и найдем ускорение точки 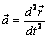, тогда уравнение (1.2) примет вид:

. (1.3)

Равенство (1.3) представляет собой дифференциальное уравнение движения материальной точки в векторной форме. Оно эквивалентно трем скалярным уравнениям, зависящим от выбора координатных осей, на которые проецируется основное уравнение динамики (1.2). Спроецируем это уравнение на оси неподвижной декартовой системы координат, учитывая, что проекции ускорения 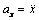, , 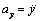, и получим

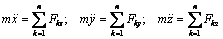, (1.4)

где x, y, z – декартовы координаты точки.

При использовании естественной формы описания движения точки спроецируем уравнение (1.2) на оси естественного трехгранника. Из кинематики известны выражения для проекций ускорения точки на касательную τ, нормаль n и бинормаль b

,

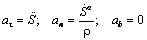учитывая которые, получим

, (1.5)

где S = S (t) – закон движения точки по траектории; ρ – радиус кривизны траектории в текущей точке. Из последнего уравнения (1.5) следует, что равнодействующая сил, приложенных к точке, лежит в соприкасающейся плоскости τ n.

При решении первой задачи динамики, когда закон движения точки известен, беря производные, можно определить левые части уравнений движения (1.4) или (1.5). В этом случае получим систему линейных алгебраических уравнений относительно неизвестных сил.

При решении второй задачи динамики известны силы, действующие на материальную точку, т.е. правые части уравнений (1.4) или (1.5), которые в данном случае являются дифференциальными уравнениями относительно декартовых или естественной координат точки. Интегрирование этих уравнений позволяет определить закон движения точки.

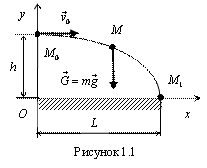
Пример. Материальная точка М массой m движется под действием силы тяжести в среде без сопротивления. В начальный момент она находилась на высоте h над поверхностью Земли и имела горизонтально направленную скорость .

Определить расстояние L, которое пройдет точка в горизонтальном направлении до момента касания поверхности Земли.

Введем неподвижную декартову систему координат, у которой ось x направлена горизонтально и параллельна начальной скорости , а ось y вертикальна и проходит через начальное положение точки М ₀(рис. 1.1). Очевидно, что движение точки будет происходить в вертикальной плоскости xOy, поэтому 3-ю координатную ось вводить не будем. На точку действует сила тяжести 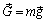, проекции которой на координатные оси и . Дифференциальные уравнения движения (1.4) примут вид:

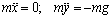
или

.

Проинтегрируем эти уравнения:

;

(1.6)

.

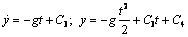Для определения постоянных интегрирования используем начальные условия:

при t = 0 . (1.7)

Из уравнений (1.6) получим

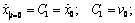
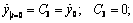
Подставим постоянные в систему уравнений (1.6) и найдем зависимости проекций скорости 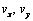и координат x, y точки от времени:

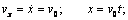
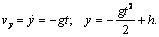
В момент касания поверхности Земли координата точки y = 0, поэтому время полета t ₁ определим из уравнения

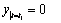или ,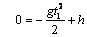

откуда получим 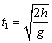. Теперь определим расстояние L, т.е. горизонтальную дальность полета точки

.

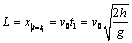Date: 2015-09-03; view: 309; Нарушение авторских прав