Момент силы и пары. Теорема о парах

Система сил, линии действия которых, лежат в одной плос­кости, называется плоской системой сил.

При изучении плоской системы сил необходимо ввести поня­тия о моменте силы относительно точки, о паре сил и ее моменте.

Моментом силы относительно точки называется взятое со знаком "плюс" или "минус" произведение модуля силы на ее пле­чо относительно данной точки. Плечом силы относительно точки называется длина перпендикуляра, опущенного из данной точки на линию действия силы. Принято следующее правило знаков: мо­мент силы относительно данной точки положителен, если сила стремится вращать тело вокруг этой точки против часовой стрел­ки, и от­рицателен в противоположном случае. Если линия дейст­вия силы проходит че­рез некоторую точку, то относительно этой точки плечо силы и ее момент равны нулю. Момент силы относительно точки определяется по формуле (рис. 1.14 ):

.

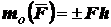Парой сил называется совокупность двух равных по модулю, параллель­ных и противонаправленных сил. Расстояние между ли­ниями действия сил пары на­зывается ее плечом. Моментом пары называется взятое со знаком "плюс" или "минус" произведение модуля сил, образующих пару, на ее плечо. Момент пары сил по­ложителен, если пара стремится вращать тело против часовой стрелки, и отрицателен в противоположном случае. Мо­мент пары определяется по формуле (рис. 1.15):

,

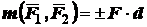где .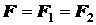

Важнейшее свойство пары сил выражается теоремой об эквивалент­ности пар, которую мы приводим без доказательства: все пары сил, лежащие в одной плоскости и имеющие одинаковые по вели­чине и знаку моменты, эквива­лентны. Из теоремы следует, что действие пары сил на твердое тело полно­стью определяется ее моментом. Не изменяя действие пары на твер­дое тело, мы можем изменять величину, направления и линии действиявходящих в нее сил, сохраняя неизменным момент пары. Таким образом, пара сил качественно отличается от простой со­вокупности двух сил, которые, как мы знаем, можно переносить только вдоль линий действия.

Два других свойства пары сил, необходимые при решении задач:

алгебраическая сумма проекций обеих сил, составляющих па­ру, на любую ось равна нулю;

алгебраическая сумма моментов обеих сил, составляющих пару, относи­тельно любой точки в плоскости пары равна моменту самой пары.

Пользуясь теоремой об эквивалентности пар, можно доказать теорему о сложении пар: любую систему пар, лежащих в одной плоскости, можно заме­нить равнодействующей парой, момент которой равен алгебраической сумме моментов слагаемых пар.

16 две меры механического движения - количество движения (импульс), выражающееся зависимостью mV и кинетическая энергия, выражающаяся зависимостью mV^2/2, что вносит неопределенность в природу этого движения.

движение материального тела (или точки) можно мерить двояким образом: количеством движения - произведением массы тела на его скорость (mv) и кинетической энергией - полупроизведением массы тела на квадрат его скорости (mv²/2). Первая мера движения векторная (в результате произведения скалярной величины - массы на векторную- скорость получается векторная величина), вторая мера движения скалярная (квадрат вектора скорости, т. е. произведение вектора самого на себя есть скалярная величина).

Аналогично двум мерам движения существуют две меры действия сил. Действие силы на тело (или точку) можно измерять или импульсом силы или работой. Импульс - векторная мера действия силы, работа - скалярная.

В динамике точки (а следовательно, и в динамике поступательного движения твердого тела) есть две важные теоремы. Это - теорема об изменении количества движения

mv-mv₀=∫Fdt,

которая гласит: "Изменение количества движения материального тела за некоторый промежуток времени равняется импульсу всех сил, действующих на тело за тот же промежуток времени", и теорема об изменении кинетической энергии:

которая читается так: "Изменение кинетической энергии тела на некотором участке пути равняется работе всех сил, действующих на тело, на том же участке пути". Рассказывая об этих теоремах, надо все время подчеркивать, что они не формальные математические записи, а физические законы, устанавливающие соотношения между мерами механического движения и мерами действия сил.

Date: 2015-09-03; view: 910; Нарушение авторских прав