Стандартные носители

1.кортежи ;

2. ограниченные последовательности ;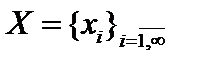

3. множество непрерывных или непрерывно дифференцируемых функций на сегменте .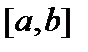

Стандартные метрики (нормы)

1. Гёльдеровские (радикальные) метрики: или ил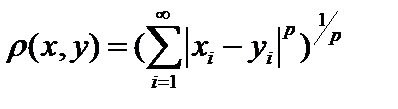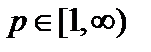и , .При 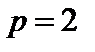эти метрики иногда называют энергетическими, так как в прикладных задачах они связана с энергией.

2. Чебышевские (супремальные), или равномерные, метрики. или .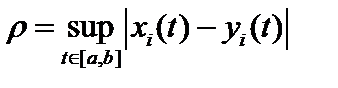

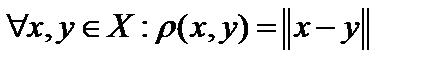Расстояние в нормированном пространстве определим так: . Нормированное пространство всегда метрическое с метрикой . Обратное, вообще говоря, неверно, то есть не любая метрика может быть нормой. При метрики становятся нормами, то есть норма элемента 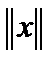это расстояние между элементом и нулевым элементом для стандартных пространств.

Пример. Метрика 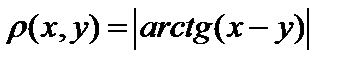- не может быть нормой при 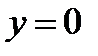, т.к. .

Действительно, две первые аксиомы метрики, очевидно, выполняются. Покажем, что выполнена и третья, то есть покажем, что 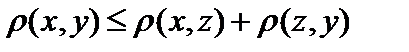: 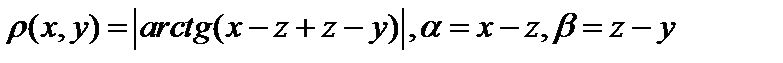. Таким образом, осталось показать, что 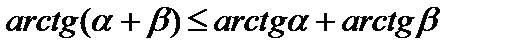. Зафиксируем 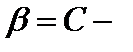произвольная константа, и рассмотрим функцию 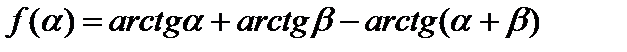. Так как , то при функция возрастает. Но если взять , , то , а . Поэтому .

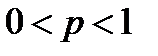Пример. Показать, что в пространстве не является нормой при и .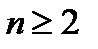

Не выполняется третья аксиома нормы. Действительно, возьмем вектор 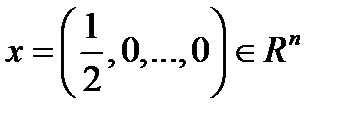и вектор . Тогда для любого и . Однако . Поскольку 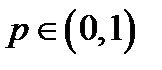, то и 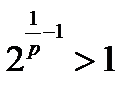. Следовательно, .

Пример. Рассмотрим пространство .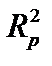

При 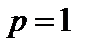норма элемента- ||x||₁ = |x| + |y| называется октаэдрической, потому что единичной сферой в трёхмерном случае 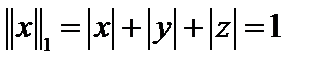будет октаэдр.

При - норма элемента ||x||₂ = (|x|² + |y|²)^1/2 – евклидова (сферическая) норма, потому что единичной сферой в трёхмерном случае будет обычная сфера.

Чебышёвская (кубическая) норма: ||x||_∞=max{|x|,|y|}, потому что единичной сферой в трёхмерном случае 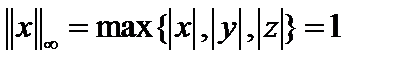будет куб.

При гёльдеровская группа норм стремится к чебышевской.

Date: 2015-09-03; view: 410; Нарушение авторских прав